
【题目】①如图1:A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点的位置(保留作图痕迹).
②如图2:某地有两个工厂M、N和两条相交叉的公路a,b现计划修建一座物资仓库,希望仓库到两个工厂的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.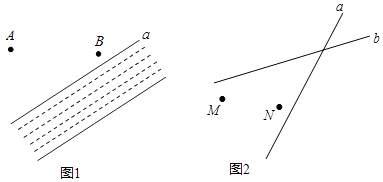
【答案】解:①如图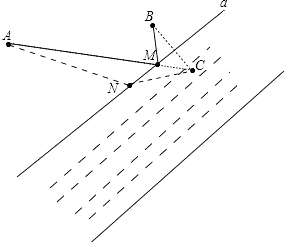
作出B的对称点C,连接AC与a交于点M,M就是抽水站的位置.
假设N点(不与点M重合)即是所求,而AN+NC>AM+BM,所以假设不成立.
点M即是所求抽水站的位置.
②如图
作出∠AOB的角平分线与MN的垂直平分线交于点P,P点就是所求的物资仓库.
【解析】①运用轴对称的性质作出B的对称点C,连接AC与a交于点M,M就是抽水站的位置.及三角形的三边关系【假设N点(不与点M重合)即是所求,而AN+NC>AM+BM,所以假设不成立】解决第一个问题;
②作出角平分线(∠AOB的角平分线)和线段垂直平分线(MN的垂直平分线)交于点P,利用它们的性质来解决第二问.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上,以及对作轴对称图形的理解,了解画对称轴图形的方法:①标出关键点②数方格,标出对称点③依次连线.


科目:初中数学 来源: 题型:
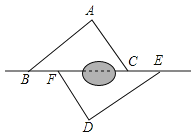
【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF
(1)根据题意,补全原形;
(2)求证:BE=DF.

查看答案和解析>>
科目:初中数学 来源: 题型:
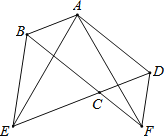
【题目】如图,在ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.
(1)求证:AE=AF;
(2)求∠EAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A.a5+a5=a10
B.﹣a6(﹣a)4=a10
C.(﹣bc)4÷(﹣bc)2=b2c2
D.(﹣ab)2a=﹣a3b2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com