练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，平行四边形ABCD的对角线AC、BD相交于点O，E，F分别是OA，OC的中点，连接BE，DF

    （1）根据题意，补全原形；

    （2）求证：BE=DF．

    【答案】（1）作图见解析；（2）证明见解析．

    【解析】

    试题分析：（1）如图所示；

    （2）由全等三角形的判定定理SAS证得△BEO≌△DFO，得出全等三角形的对应边相等即可．

    试题解析：（1）解：如图所示：

    （2）证明：∵四边形ABCD是平行四边形，对角线AC、BD交于点O，∴OB=OD，OA=OC．

    又∵E，F分别是OA、OC的中点，∴OE=OA，OF=OC，∴OE=OF．

    在△BEO与△DFO中，∵OE=OF，∠BOE=∠DOF，OB=OD，∴△BEO≌△DFO（SAS），∴BE=DF．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】二次函数y=3(x -5)2的图象上有两点P(2，y1)，Q(6，y2)，则y1和y2的大小关系是__________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ABC=90°，AB=CB，以AB为直径的⊙O交AC于点D，点E是AB边上一点（点E不与点A、B重合），DE的延长线交⊙O于点G，DF⊥DG，且交BC于点F．

    （1）求证：AE=BF；

    （2）连接GB，EF，求证：GB∥EF；

    （3）若AE=1，EB=2，求DG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD的对角线AC，BD交于点O，△AOD是正三角形，AD=4，则平行四边形ABCD的面积为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】化简求值：已知：（x﹣3）2 =0，求3x2y﹣[2xy2﹣2（xy﹣ ）+3xy]+5xy2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

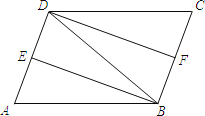
    【题目】如图，在ABCD中，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F，连接BD．

    （1）求证：△ABE≌△CDF；

    （2）若AB=DB，求证：四边形DFBE是矩形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果两个数m、n互为相反数，那么下列结论不正确的是（ ）
    A.m+n=0
    B.
    C.|m|=|n|
    D.数轴上，表示这两个数的点到原点的距离相等

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】①如图1：A、B是两个蓄水池，都在河流a的同侧，为了方便灌溉作物，要在河边建一个抽水站，将河水送到A、B两地，问该站建在河边什么地方，可使所修的渠道最短，试在图中确定该点的位置（保留作图痕迹）．
    ②如图2：某地有两个工厂M、N和两条相交叉的公路a，b现计划修建一座物资仓库，希望仓库到两个工厂的距离相等，到两条公路的距离也相等．你能确定仓库应该建在什么位置吗？在所给的图形中画出你的设计方案．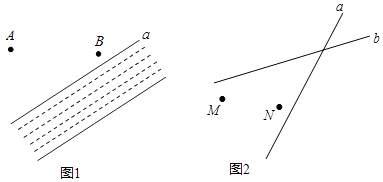

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知直线PQ∥MN，点A在直线PQ上，点C、D在直线MN上，连接AC、AD，∠PAC=50°，∠ADC=30°，AE平分∠PAD，CE平分∠ACD，AE与CE相交于E．
    （1）求∠AEC的度数；
    （2）若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置，此时A1E平分∠AA1D1 ， CE平分∠ACD1 ， A1E与CE相交于E，∠PAC=50°，∠A1D1C=30°，求∠A1EC的度数．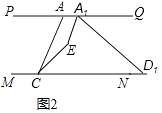
    （3）若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置，其他条件与（2）相同，求此时∠A1EC的度数．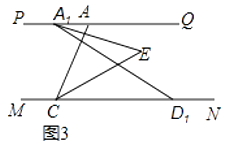

    查看答案和解析>>

    同步练习册答案