
����Ŀ����ͼ1����ֱ֪��PQ��MN����A��ֱ��PQ�ϣ���C��D��ֱ��MN�ϣ�����AC��AD����PAC=50�㣬��ADC=30�㣬AEƽ�֡�PAD��CEƽ�֡�ACD��AE��CE�ཻ��E�� 
��1�����AEC�Ķ�����
��2������ͼ1�е��߶�AD��MN����ƽ�Ƶ�A1D1��ͼ2��ʾλ�ã���ʱA1Eƽ�֡�AA1D1 �� CEƽ�֡�ACD1 �� A1E��CE�ཻ��E����PAC=50�㣬��A1D1C=30�㣬���A1EC�Ķ����� 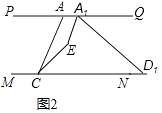
��3������ͼ1�е��߶�AD��MN����ƽ�Ƶ�A1D1��ͼ3��ʾλ�ã����������루2����ͬ�����ʱ��A1EC�Ķ����� 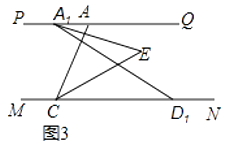
���𰸡�
��1���⣺��ͼ1��ʾ��
��ֱ��PQ��MN����ADC=30�㣬
���ADC=��QAD=30�㣬
���PAD=150�㣬
�ߡ�PAC=50�㣬AEƽ�֡�PAD��
���PAE=75�㣬
���CAE=25�㣬
�ɵá�PAC=��ACN=50�㣬
��CEƽ�֡�ACD��
���ECA=25�㣬
���AEC=180�㩁25�㩁25��=130�㣻
��2���⣺��ͼ2��ʾ��
�ߡ�A1D1C=30�㣬�߶�AD��MN����ƽ�Ƶ�A1D1��PQ��MN��
���QA1D1=30�㣬
���PA1D1=150�㣬
��A1Eƽ�֡�AA1D1��
���PA1E=��EA1D1=75�㣬
�ߡ�PAC=50�㣬PQ��MN��
���CAQ=130�㣬��ACN=50�㣬
��CEƽ�֡�ACD1��
���ACE=25�㣬
���CEA1=360�㩁25�㩁130�㩁75��=130�㣻
��3���⣺��ͼ3��ʾ������E��FE��PQ��

�ߡ�A1D1C=30�㣬�߶�AD��MN����ƽ�Ƶ�A1D1��PQ��MN��
���QA1D1=30�㣬
��A1Eƽ�֡�AA1D1��
���QA1E=��2=15�㣬
�ߡ�PAC=50�㣬PQ��MN��
���ACN=50�㣬
��CEƽ�֡�ACD1��
���ACE=��ECN=��1=25�㣬
���CEA1=��1+��2=15��+25��=40��
����������1��ֱ�����ý�ƽ���ߵ����ʽ��ƽ���ߵ����ʵó���CAE�Լ���ECA�Ķ����������ó��𰸣���2��ֱ�����ý�ƽ���ߵ����ʽ��ƽ���ߵ����ʵó���CAE�Լ���ECA�Ķ����������ó��𰸣���3��ֱ�����ý�ƽ���ߵ����ʽ��ƽ���ߵ����ʵó���1�͡�2�Ķ����������ó��𰸣�
�����㾫����������Ҫ������ƽ���ߵ����ʺ�ƽ�Ƶ����ʵ����֪ʶ�㣬��Ҫ������ֱ��ƽ�У�ͬλ����ȣ���ֱ��ƽ�У��ڴ�����ȣ���ֱ��ƽ�У�ͬ���ڽǻ������پ���ƽ��֮���ͼ����ԭ����ͼ�εĶ�Ӧ�߶�ƽ�У�����ͬһֱ���ϣ�����ȣ���Ӧ����ȣ�ͼ�ε���״���С��û�з����仯���ھ���ƽ�ƺ�Ӧ���������߶�ƽ�У�����ͬһֱ���ϣ�����Ȳ�����ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��E��F�ֱ���OA��OC���е㣬����BE��DF
��1���������⣬��ȫԭ�Σ�
��2����֤��BE=DF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a3��2a2+a�ֽ���ʽ�Ľ���ǣ� ��
A.a2��a��2��+a
B.a��a2��2a��
C.a��a+1����a��1��
D.a��a��1��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ�������
A.a5+a5=a10
B.��a6����a��4=a10
C.����bc��4�£���bc��2=b2c2
D.����ab��2a=��a3b2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC �� DΪ��BC��һ�㣬��AB��BDΪ�ڱ���ƽ���ı���ABDE �� ����AD��EC �� ��BD��CD �� ��֤���ı���ADCE�Ǿ��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x��y��������ʽ���д�����ǣ� ��
A.x+ ![]() ��y+
��y+ ![]()
B.x��3��y��3
C.![]() ��
�� ![]()
D.��3x����3y
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�dz�����ֽ������DEF=10�㣬��ֽ����EF�۵���ͼ2������BF�۵���ͼ3����ͼ3�С�CFE�����Ƕ��٣� �� 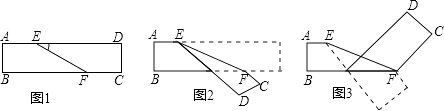
A.160��
B.150��
C.120��
D.110��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCDΪƽ���ı��Σ���BAD�Ľ�ƽ����AE��CD�ڵ�F����BC���ӳ����ڵ�E��
��1����֤��BE=CD��
��2������BF����BF��AE����BEA=60�㣬AB=4����ƽ���ı���ABCD�������
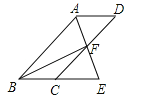
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com