练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图1是长方形纸带，∠DEF=10°，将纸带沿EF折叠成图2，再沿BF折叠成图3，则图3中∠CFE度数是多少（ ）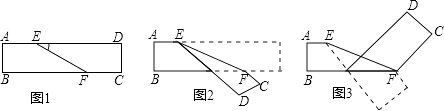
    A.160°
    B.150°
    C.120°
    D.110°

    【答案】B
    【解析】解：∵四边形ABCD为长方形，

    ∴AD∥BC，

    ∴∠BFE=∠DEF=10°．

    由翻折的性质可知：

    ∠EFC=180°﹣∠BFE=170°，∠BFC=∠EFC﹣∠BFE=160°，∠CFE=∠BFC﹣∠BFE=150°．

    故选B．

    【考点精析】通过灵活运用矩形的性质和翻折变换（折叠问题），掌握矩形的四个角都是直角，矩形的对角线相等；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如果两个数m、n互为相反数，那么下列结论不正确的是（ ）
    A.m+n=0
    B.
    C.|m|=|n|
    D.数轴上，表示这两个数的点到原点的距离相等

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于点E，DF⊥AC于点F，△ABC的面积是28cm2 ， AB=16cm，AC=12cm，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知直线PQ∥MN，点A在直线PQ上，点C、D在直线MN上，连接AC、AD，∠PAC=50°，∠ADC=30°，AE平分∠PAD，CE平分∠ACD，AE与CE相交于E．
    （1）求∠AEC的度数；
    （2）若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置，此时A1E平分∠AA1D1 ， CE平分∠ACD1 ， A1E与CE相交于E，∠PAC=50°，∠A1D1C=30°，求∠A1EC的度数．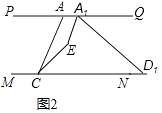
    （3）若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置，其他条件与（2）相同，求此时∠A1EC的度数．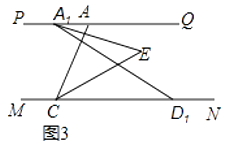

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=﹣x2﹣x+2与x轴交于A、B两点，与y轴交于点C

    （1）求点A，B，C的坐标；

    （2）点E是此抛物线上的点，点F是其对称轴上的点，求以A，B，E，F为顶点的平行四边形的面积；

    （3）此抛物线的对称轴上是否存在点M，使得△ACM是等腰三角形？若存在，请求出点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题正确的是（ ）.

    A.等弧对等弦；B.在同圆中，相等的弦所对的圆周角相等；

    C.平分弦的直径垂直于弦；D.经过切点的直线是圆的切线.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠DAB+∠D=180°，AC平分∠DAB，且∠CAD=25°，∠B=95°．求：∠DCE和∠DCA的度数．
    请将以下解答补充完整，
    解：因为∠DAB+∠D=180°
    所以DC∥AB（）
    所以∠DCE=∠B（）
    又因为∠B=95°，
    所以∠DCE=°；
    因为AC平分∠DAB，∠CAD=25°，根据角平分线定义，
    所以∠CAB==°，
    因为DC∥AB
    所以∠DCA=∠CAB，（）
    所以∠DCA=°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列两个图形一定相似的是（ ）

    A.矩形B.有一个内角为100°的等腰三角形

    C.直角三角形D.菱形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题是真命题的是（ ）

    A. 菱形的对角线互相平分 B. 一组对边平行的四边形是平行四边形

    C. 对角线互相垂直且相等的四边形是正方形 D. 对角线相等的四边形是矩形

    查看答案和解析>>

    同步练习册答案