
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.

(1)求证:AE=BF;
(2)连接GB,EF,求证:GB∥EF;
(3)若AE=1,EB=2,求DG的长.
【答案】(1)详见解析;(2)详见解析;(3)![]() .
.
【解析】
试题分析:(1)连接BD,由三角形ABC为等腰直角三角形,求出∠A与∠C的度数,根据AB为圆的直径,利用圆周角定理得到∠ADB为直角,即BD垂直于AC,利用直角三角形斜边上的中线等于斜边的一半,得到AD=DC=BD=![]() AC,进而确定出∠A=∠FBD,再利用同角的余角相等得到一对角相等,利用ASA得到三角形AED与三角形BFD全等,利用全等三角形对应边相等即可得证;(2)连接EF,BG,由三角形AED与三角形BFD全等,得到ED=FD,进而得到三角形DEF为等腰直角三角形,利用圆周角定理及等腰直角三角形性质得到一对同位角相等,利用同位角相等两直线平行即可得证;(3)由全等三角形对应边相等得到AE=BF=1,在直角三角形BEF中,利用勾股定理求出EF的长,利用锐角三角形函数定义求出DE的长,利用两对角相等的三角形相似得到三角形AED与三角形GEB相似,由相似得比例,求出GE的长,由GE+ED求出GD的长即可.
AC,进而确定出∠A=∠FBD,再利用同角的余角相等得到一对角相等,利用ASA得到三角形AED与三角形BFD全等,利用全等三角形对应边相等即可得证;(2)连接EF,BG,由三角形AED与三角形BFD全等,得到ED=FD,进而得到三角形DEF为等腰直角三角形,利用圆周角定理及等腰直角三角形性质得到一对同位角相等,利用同位角相等两直线平行即可得证;(3)由全等三角形对应边相等得到AE=BF=1,在直角三角形BEF中,利用勾股定理求出EF的长,利用锐角三角形函数定义求出DE的长,利用两对角相等的三角形相似得到三角形AED与三角形GEB相似,由相似得比例,求出GE的长,由GE+ED求出GD的长即可.
试题解析:(1)证明:连接BD,
在Rt△ABC中,∠ABC=90°,AB=BC,
∴∠A=∠C=45°,
∵AB为圆O的直径,
∴∠ADB=90°,即BD⊥AC,
∴AD=DC=BD=![]() AC,∠CBD=∠C=45°,
AC,∠CBD=∠C=45°,
∴∠A=∠FBD,
∵DF⊥DG,
∴∠FDG=90°,
∴∠FDB+∠BDG=90°,
∵∠EDA+∠BDG=90°,
∴∠EDA=∠FDB,
在△AED和△BFD中,
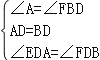 ,
,
∴△AED≌△BFD(ASA),
∴AE=BF;
(2)证明:连接EF,BG,
∵△AED≌△BFD,
∴DE=DF,
∵∠EDF=90°,
∴△EDF是等腰直角三角形,
∴∠DEF=45°,
∵∠G=∠A=45°,
∴∠G=∠DEF,
∴GB∥EF;
(3)∵AE=BF,AE=1,
∴BF=1,
在Rt△EBF中,∠EBF=90°,
∴根据勾股定理得:EF2=EB2+BF2,
∵EB=2,BF=1,
∴EF=![]() =
=![]() ,
,
∵△DEF为等腰直角三角形,∠EDF=90°,
∴cos∠DEF=![]() ,
,
∵EF=![]() ,
,
∴DE=![]() ×
×![]() =
=![]() ,
,
∵∠G=∠A,∠GEB=∠AED,
∴△GEB∽△AED,
∴![]() =
=![]() ,即GEED=AEEB,
,即GEED=AEEB,
∴![]() GE=2,即GE=
GE=2,即GE=![]() ,
,
则GD=GE+ED=![]() .
.



 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
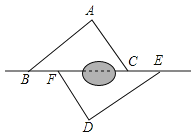
【题目】如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC. 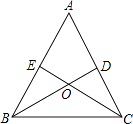
(1)上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC与Rt△DEF的位置如图所示,其中AC=2![]() ,BC=6,DE=3
,BC=6,DE=3![]() ,∠D=30°,其中,Rt△DEF沿射线CB以每秒1个单位长度的速度向右运动,射线DE、DF与射线AB分别交于N、M两点,运动时间为t,当点E运动到与点B重合时停止运动.
,∠D=30°,其中,Rt△DEF沿射线CB以每秒1个单位长度的速度向右运动,射线DE、DF与射线AB分别交于N、M两点,运动时间为t,当点E运动到与点B重合时停止运动.
(1)当Rt△DEF在起始时,求∠AMF的度数;
(2)设BC的中点的为P,当△PBM为等腰三角形时,求t的值;
(3)若两个三角形重叠部分的面积为S,写出S与t的函数关系式和相应的自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
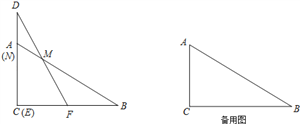
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF
(1)根据题意,补全原形;
(2)求证:BE=DF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com