
【题目】定义新运算“※”:a※b=2a+b则下列结论:①(-2)※5=1;②若x※(x-6)=0,则![]() ;③存在有理数y,使y※(y+1)=y※(y-1)成立;④若m※n=5,m※(-n)=3,则
;③存在有理数y,使y※(y+1)=y※(y-1)成立;④若m※n=5,m※(-n)=3,则![]() ,
,![]() 其中正确的是 _______________(把所有正确结论的序号都选上).
其中正确的是 _______________(把所有正确结论的序号都选上).
【答案】①②④
【解析】
①根据新运算“※”的运算公式进行运算即可得出结论;
②根据新运算“※”的运算公式将方程进行变形,解出关于x的一元一次方程;
③分别求出y※(y+1)和y※(y-1)即可得出答案;
④根据新运算“※”的运算公式将方程进行变形,即可得出关于m、n的二元一次方程,解之即可得出结论.
解:①(-2)※5=2×(-2)+5=1;
②x※(x-6)=2x+x-6=3x-6=0,解得x=2;
③∵y※(y+1)=2y+y+1=3y+1,y※(y-1)=2y+y-1=3y-1,
∵y※(y+1)=y※(y-1)
∵3y+1=3y-1无解,
∴y※(y+1)=y※(y-1)不成立;
④∵m※n=2m+n=5,m※(-n)=2m-n=3,
∴![]() 解得
解得![]() .
.
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】某学校组织了“热爱宪法,捍卫宪法”的知识竞赛,赛后发现所有学生的成绩(总分100分)均不低于50分,为了解本次竞赛的成绩分布情况,随机抽取若干名学生的成绩作为样本进行整理,并绘制了不完整的统计图表,请你根据统计图表解答下列问题.
学校若干名学生成绩分布统计表
分数段(成绩为x分) | 频数 | 频率 |
50≤x<60 | 16 | 0.08 |
60≤x<70 | a | 0.31 |
70≤x<80 | 72 | 0.36 |
80≤x<90 | c | d |
90≤x≤100 | 12 | b |
(1)此次抽样调查的样本容量是 ;
(2)写出表中的a= ,b= ,c= ;
(3)补全学生成绩分布直方图;
(4)比赛按照分数由高到低共设置一、二、三等奖,若有25%的参赛学生能获得一等奖,则一等奖的分数线是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
查看答案和解析>>
科目:初中数学 来源: 题型:
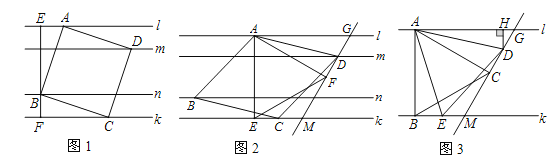
【题目】【背景】已知:l∥m∥n∥k,平行线l与m、m与n、n与k之间的距离分别为d1,d2,d3,且d1=d3=1,d2=2.我们把四个顶点分别在l,m,n,k这四条平行线上的四边形称为“格线四边形” .
【探究1】(1)如图1,正方形ABCD为“格线四边形”,BE⊥l于点E,BE的反向延长线交直线k于点F.求正方形ABCD的边长.
【探究2】(2)如图2,菱形ABCD为“格线四边形”且∠ADC=60°,△AEF是等边三角形,AE⊥k于点E,∠AFD=90°,直线DF分别交直线l,k于点G、点M.求证:EC=DF.
【拓展】(3)如图3,l∥k,等边△ABC的顶点A,B分别落在直线l,k上,AB⊥k于点B,且∠ACD=90°,直线CD分别交直线l、k于点G、点M,点D、点E分别是线段GM、BM上的动点,且始终保持AD=AE,DH⊥l于点H.猜想:DH在什么范围内,BC∥DE?并说明此时BC∥DE的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,我国很多地区持续出现雾霾天气.某社区为了调查本社区居民对雾霾天气主要成因的认识情况,随机对该社区部分居民进行了问卷调查,要求居民从五个主要成因中只选择其中的一项,被调查居民都按要求填写了问卷.社区对调查结果进行了整理,绘制了如下不完整的统计图表.被调查居民选择各选项人数统计表
雾霾天气的主要成因 | 频数(人数) |
A大气气压低,空气不流动 | m |
B地面灰尘大,空气湿度低 | 40 |
C汽车尾气排放 | n |
D工厂造成的污染 | 120 |
E其他 | 60 |
请根据图表中提供的信息解答下列问题:

(1)填空:m=________,n=________,扇形统计图中C选项所占的百分比为________.
(2)若该社区居民约有6 000人,请估计其中会选择D选项的居民人数.
(3)对于“雾霾”这个环境问题,请你用简短的语言发出倡议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张师傅开车到某地送货,汽车出发前油箱中有油50升,行驶一段时间,张师傅在加油站加油,然后继续向目的地行驶.已知加油前、后汽车都匀速行驶,汽车行驶时每小时的耗油量一定.油箱中剩余油量Q(升)与汽车行驶时间t(时)之间的函数图象如图所示.

(1)张师傅开车行驶________小时后开始加油,本次加油________升.
(2)求加油前Q与t之间的函数关系式.
(3)如果加油站距目的地210千米,汽车行驶速度为70千米/时,张师傅要想到达目的地,油箱中的油是否够用?请通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,DE垂直平分AB ,分别交AB、BC于点D 、E,MN垂直平分AC,分别交AC、BC于点M、N,连接AE,AN.
(1)如图1,若∠BAC= 100°,求∠EAN的度数;
(2)如图2,若∠BAC=70°,求∠EAN的度数;
(3)若∠BAC=a(a≠90°),请直接写出∠EAN的度数. (用含a的代数式表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com