
【题目】如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF.
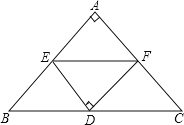
(1)若设BE=a,CF=b,满足![]() +|b﹣5|=
+|b﹣5|=![]() +
+![]() ,求BE及CF的长.
,求BE及CF的长.
(2)求证:BE2+CF2=EF2.
(3)在(1)的条件下,求△DEF的面积.
【答案】(1)BE=12,CF=5;(2)见解析;(3)![]() .
.
【解析】
试题分析:(1)先根据二次根式的非负性求出m=2,再由非负数的性质求出a、b的值,进而得到BE及CF的长;
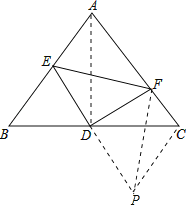
(2)延长ED到P,使DP=DE,连接FP,CP,利用SAS得到三角形BED与三角形CPD全等,利用全等三角形对应边相等得到BE=CP,再利用SAS得到△EDF和△PDF全等,利用全等三角形对应边相等得到EF=FP,利用等角的余角相等得到∠FCP为直角,在直角三角形FCP中,利用勾股定理列出关系式,等量代换即可得证;
(3)连接AD,由AB=AC,且D为BC的中点,利用三线合一得到AD垂直于BC,AD为角平分线,再由三角形ABC为等腰直角三角形,得到一对角相等,利用同角的余角相等得到一对角相等,再由AD=CD,利用ASA得到三角形AED与三角形CFD全等,利用全等三角形对应边相等得到AE=CF=5,DE=DF,由AE+EB求出AB的长,即为AC的长,再由AC﹣CF求出AF的长,在直角三角形AEF中,利用勾股定理求出EF的长,再根据三角形DEF为等腰直角三角形求出DE与DF的长,即可确定出三角形DEF的面积.
(1)解:由题意得![]() ,
,
解得m=2,
则![]() +|b﹣5|=0,
+|b﹣5|=0,
所以a﹣12=0,b﹣5=0,
a=12,b=5,
即BE=12,CF=5;
(2)证明:延长ED到P,使DP=DE,连接FP,CP,
在△BED和△CPD中,
 ,
,
∴△BED≌△CPD(SAS),
∴BE=CP,∠B=∠CDP,
在△EDF和△PDF中,
 ,
,
∴△EDF≌△PDF(SAS),
∴EF=FP,
∵∠B=∠DCP,∠A=90°,
∴∠B+∠ACB=90°,
∴∠ACB+∠DCP=90°,即∠FCP=90°,
在Rt△FCP中,根据勾股定理得:CF2+CP2=PF2,
∵BE=CP,PF=EF,
∴BE2+CF2=EF2;
(3)解:连接AD,
∵△ABC为等腰直角三角形,D为BC的中点,
∴∠BAD=∠FCD=45°,AD=BD=CD,AD⊥BC,
∵ED⊥FD,
∴∠EDA+∠ADF=90°,∠ADF+∠FDC=90°,
∴∠EDA=∠FDC,
在△AED和△CFD中,
 ,
,
∴△AED≌△CFD(ASA),
∴AE=CF=5,DE=DF,即△EDF为等腰直角三角形,
∴AB=AE+EB=5+12=17,
∴AF=AC﹣FC=AB﹣CF=17﹣5=12,
在Rt△EAF中,根据勾股定理得:EF=![]() =13,
=13,
设DE=DF=x,
根据勾股定理得:x2+x2=132,
解得:x=![]() ,即DE=DF=
,即DE=DF=![]() ,
,
则S△DEF=![]() DEDF=
DEDF=![]() ×
×![]() ×
×![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况、他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图:
分组 | 频数 | 百分比 |
600≤x<800 | 2 | 5% |
800≤x<1000 | 6 | 15% |
1000≤x<1200 | 45% | |
9 | 22.5% | |
1600≤x<1800 | 2 | |
合计 | 40 | 100% |
根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
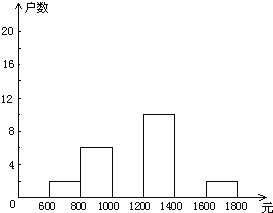
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为4,B是⊙O外一点,连接BO,且BO=6,延长BO交⊙O于点A,D是⊙O上一点,过点A作直线BD的垂线AC,垂足为C,连接AD,且AD平分∠BAC .
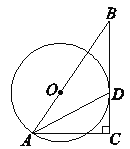
(1)求证:BD是⊙O的切线 ;
(2)求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将△ABC水平向右平移5个单位得到△A′B′C′.
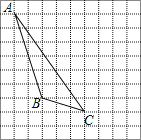
(1)补全△A′B′C′;利用网格点和直尺画图:
(2)画出AB边上的高线CD;
(3)图中△ABC的面积是 ;
(4)△ABC与△EBC面积相等,在图中描出所有满足条件且异于A点的格点E,并记为E1E2E3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.
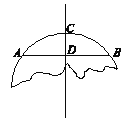
(1)求作此残片所在的⊙O(不写作法,保留作图痕迹);
(2)已知AB=12cm,(1)中⊙O的直径为20cm,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=﹣x2+4x(单位:米)的一部分,则水喷出的最大高度是( )

A.4米 B.3米 C.2米 D.1米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com