
分析 注意到这些分数是分组依次向后排列的:
第一组:$\frac{1}{1}$,
第二组:$\frac{1}{2}$,$\frac{2}{2}$,$\frac{1}{2}$
第三组:$\frac{1}{3}$,$\frac{2}{3}$,$\frac{3}{3}$,$\frac{2}{3}$,$\frac{1}{3}$
第四组:$\frac{1}{4}$,$\frac{2}{4}$,$\frac{3}{4}$,$\frac{4}{4}$,$\frac{3}{4}$,$\frac{2}{4}$,$\frac{1}{4}$,
…
依此类推.
每一组的中心分数的分子分母相同;
每一组分数的分母一样,分子从中心分数开始向两边依次递减;
每一组分数的个数依次为:1,3,5,7,9,…(2n-1);
每n组的中心分数排在该组的第n个;
前n组的分数总个数为:1+3+5+7+…+(2n-1)=n2;
基于上述分析,答案易得.
解答 解:将这列分数分组如下:
第一组:$\frac{1}{1}$,
第二组:$\frac{1}{2}$,$\frac{2}{2}$,$\frac{1}{2}$
第三组:$\frac{1}{3}$,$\frac{2}{3}$,$\frac{3}{3}$,$\frac{2}{3}$,$\frac{1}{3}$
第四组:$\frac{1}{4}$,$\frac{2}{4}$,$\frac{3}{4}$,$\frac{4}{4}$,$\frac{3}{4}$,$\frac{2}{4}$,$\frac{1}{4}$,
…
每一组的中心分数的分子分母相同;
每一组分数的分母一样,分子从中心分数开始向两边依次递减,
每一组分数的个数依次为:1,3,5,7,9,…(2n-1);
每n组的中心分数排在该组的第n个;
前n组的分数总个数为:1+3+5+7+…+(2n-1)=n2;
①前9组分数的总个数为:1+3+5+7+…+17=81,
$\frac{10}{10}$排在第十组的第10个位置,所以$\frac{10}{10}$是第91个分数;
②前17组的分数总个数为:172=289,
前18组的分数总个数为:182=324,
300-289=11,
所以,第300个分数在第18组的第11个位置,
所以,第300个分数为:$\frac{11}{18}$.
点评 本题是数字规律题,考查学生对数列变化规律的观察分析能力,有一定难度.看出数列是以分组的方式排列是解答本题的突破口和关键所在,同时解答过程用到了等差数列求和公式,这一点也需要同学们掌握.


科目:初中数学 来源: 题型:填空题
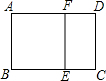 如图,已知矩形ABCD中,AD>AB,在矩形ABCD内作正方形ABEF,若四边形CEFD与矩形ABCD相似,且AB=2,则AD的长为$\sqrt{5}$+1.
如图,已知矩形ABCD中,AD>AB,在矩形ABCD内作正方形ABEF,若四边形CEFD与矩形ABCD相似,且AB=2,则AD的长为$\sqrt{5}$+1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
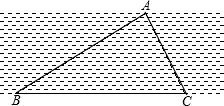 如图,B、C是河岸边两点,A是对岸边上的一点,测得∠ABC=31°,∠ACB=59°,BC=400m,求A到岸边BC的距离是多少米?(结果精确到1米).
如图,B、C是河岸边两点,A是对岸边上的一点,测得∠ABC=31°,∠ACB=59°,BC=400m,求A到岸边BC的距离是多少米?(结果精确到1米).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com