
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB=4,点P是AB边上一个动点,过点P作AB的垂线交AC边与点D,以PD为边作∠DPE=60°,PE交BC边与点E.
(1)当点D为AC边的中点时,求BE的长;
(2)当PD=PE时,求AP的长;
(3)设AP 的长为![]() ,四边形CDPE的面积为
,四边形CDPE的面积为![]() ,请直接写出
,请直接写出![]() 与
与![]() 的函数解析式及自变量
的函数解析式及自变量![]() 的取值范围.
的取值范围.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据含有30°角的直角三角形的性质和勾股定理求出![]() 的长,从而求出BP的长,然后求出BE的长;
的长,从而求出BP的长,然后求出BE的长;
(2)设AP= ![]() ,则BP=4—
,则BP=4—![]() ,根据含有30°角的直角三角形的性质和勾股定理求出PD和PE的长,再根据PD=PE列出方程即可.
,根据含有30°角的直角三角形的性质和勾股定理求出PD和PE的长,再根据PD=PE列出方程即可.
(3)分别用AP表示PD、PE、BE,再根据![]() 即可求出.
即可求出.
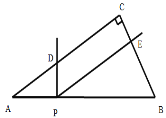
(1)在△ABC中,∠ACB=90°,∠A=30°,AB=4,
![]()
∵点D为AC边的中点
![]() ,
,
∵∠DPE=60°,过点P作AB的垂线交AC边与点D,
∴∠EPB=30°,∴EB ![]()
(2)设AP= ![]() ,则BP=4—
,则BP=4—![]() ,在两个含有30°的
,在两个含有30°的![]() 中得出:
中得出:
AD=2DP,BP=2BE,由勾股定理解得:![]() ,
,
∵PD=PE,∴![]() 解得
解得![]() 即有AP=
即有AP= ![]()
(3)由(2)知:AP= ![]() ,
,![]()



科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是△ABC的外接圆,且AB=BC=CD,AB∥CD,连接BD.
(1)求证:BD是⊙O的切线;
(2)若AB=10,cos∠BAC=![]() ,求BD的长及⊙O的半径.
,求BD的长及⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射击队为了解运动员的年龄情况,作了一次年龄调查,根据射击运动员的年龄(单位:岁),绘制出如图的统计图.
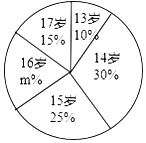
(1)求m的值;
(2)该射击队运动员年龄是众数是 .
(3)求该射击队运动员的平均年龄;
(4)若该射击队有13岁运动员2人,则该射击队中14岁运动员有几人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB中点,在“①DE=AC;②DE⊥AC;③∠EAF=∠ADE;④∠CAB=30°”这四个结论中,正确的个数有 ( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
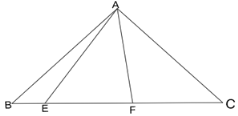
【题目】已知:如图,等腰直角三角形ABC中,∠BAC=90°,BA=AC,点E、F是线段BC上两动点且∠EAF=45°,请写出BE、EF、FC之间的等量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了全面提升中小学教师的综合素质,贵阳市将对教师的专业知识每三年进行一次考核.某校决定为全校数学教师每人购买一本义务教育《数学课程标准(2011年版)》(以下简称《标准》),同时每人配套购买一本《数学课程标准(2011年版)解读》(以下简称《解读》),其中《解读》的单价比《标准》的单价多25元.若学校购买《标准》用了378元,购买《解读》用了1053元,请问《标准》和《解读》的单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
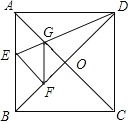
【题目】如图,正方形ABCD中,对角线AC、BD交于点O,折叠正方形纸片,使AD落在BC上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB,AC于点E、G,连结GF,给出下列结论①∠AGD=110.5°;②S△AGD=S△OGD;③四边形AEFG是菱形;④BF=![]() OF;⑤如果S△OGF=1,那么正方形ABCD的面积是12+8
OF;⑤如果S△OGF=1,那么正方形ABCD的面积是12+8![]() ,其中正确的有( )个.
,其中正确的有( )个.
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)某工厂生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本![]() (万元/吨)与产量
(万元/吨)与产量![]() (吨)之间是一次函数关系,函数
(吨)之间是一次函数关系,函数![]() 与自变量
与自变量![]() 的部分对应值如下表:
的部分对应值如下表:
| 10 | 20 | 30 |
| 45 | 40 | 35 |
(1)求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)当投入生产这种产品的总成本为1200万元时,求该产品的总产量;(注:总成本=每吨成本×总产量)
(3)市场调查发现,这种产品每月销售量![]() (吨)与销售单价
(吨)与销售单价![]() (万元/吨)之间满足如图所示的函数关系.该厂第一个月按同一销售单价卖出这种产品25吨,请求出该厂第一个月销售这种产品获得的利润.(注:利润=售价—成本)
(万元/吨)之间满足如图所示的函数关系.该厂第一个月按同一销售单价卖出这种产品25吨,请求出该厂第一个月销售这种产品获得的利润.(注:利润=售价—成本)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com