
【题目】如图,正方形ABCD中,对角线AC、BD交于点O,折叠正方形纸片,使AD落在BC上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB,AC于点E、G,连结GF,给出下列结论①∠AGD=110.5°;②S△AGD=S△OGD;③四边形AEFG是菱形;④BF=![]() OF;⑤如果S△OGF=1,那么正方形ABCD的面积是12+8
OF;⑤如果S△OGF=1,那么正方形ABCD的面积是12+8![]() ,其中正确的有( )个.
,其中正确的有( )个.
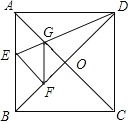
A.2个B.3个C.4个D.5个
【答案】B
【解析】
①由四边形ABCD是正方形,可得∠GAD=∠ADO=45°,又由折叠的性质,可求得∠ADG的度数,从而求得∠AGD;
②证△AEG≌△FEG得AG=FG,由FG>OG即可得;
③先计算∠AGE=∠GAD+∠ADG=67.5°,∠AED=∠AGD-∠EAG=67.5°,从而得到∠AGE=∠AED,易得AE=AG,由AE=FE、AG=FG即可得证;
④设OF=a,先求得∠EFG=45°,易得∠GFO=45°,在Rt△OFG中,GF=![]() OF=
OF=![]() a,从而可证得BF=EF=GF=
a,从而可证得BF=EF=GF=![]() OF;
OF;
⑤由S△OGF=1求出a2,再表示出BE及AE的长,利用正方形的面积公式可得出结论.
解:∵四边形ABCD是正方形,
∴∠EAG=∠GAD=∠ADO=45°,∠AOB=90°,
由折叠的性质可得:∠ADG=![]() ∠ADO=22.5°,
∠ADO=22.5°,
∴∠AGD=180°-∠GAD-∠ADG=112.5°,
故①错误;
由折叠的性质可得:AE=EF,∠AEG=∠FEG,
在△AEG和△FEG中,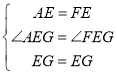 ,
,
∴△AEG≌△FEG(SAS),
∴AG=FG,
∵在Rt△GOF中,AG=FG>GO,
∴S△AGD>S△OGD,故②错误;
∵∠AGE=∠GAD+∠ADG=67.5°,∠AED=∠AGD-∠EAG=67.5°,
∴∠AGE=∠AED,
∴AE=AG,
又∵AE=FE,AG=FG,
∴AE=EF=GF=AG,
∴四边形AEFG是菱形,故③正确;
设OF=a,
∵△AEG≌△FEG,
∴∠EFG=∠EAG=45°,
又∵∠EFO=90°,
∴∠GFO=45°,
∴在Rt△OFG中,GF=![]() OF=
OF=![]() a,
a,
∵∠EFO=90°,∠EBF=45°,
∴在Rt△EBF中,BF=EF=GF=![]() a,即BF=
a,即BF=![]() OF,故④正确;
OF,故④正确;
∵S△OGF=1,
∴![]() OF2=1,即
OF2=1,即![]() a2=1,
a2=1,
则a2=2,
∵BF=EF=![]() a,且∠BFE=90°,
a,且∠BFE=90°,
∴BE=2a,
又∵AE=EF=![]() a,
a,
∴AB=AE+BE=![]() a+2a=(2+
a+2a=(2+![]() )a,
)a,
则正方形ABCD的面积是(2+![]() )2a2=(6+
)2a2=(6+![]() )×2=12+
)×2=12+![]() ,
,
故⑤正确;
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC=6![]() ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )

A. 6 B. 3![]() C. 2
C. 2![]() D. 4.5
D. 4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB=4,点P是AB边上一个动点,过点P作AB的垂线交AC边与点D,以PD为边作∠DPE=60°,PE交BC边与点E.
(1)当点D为AC边的中点时,求BE的长;
(2)当PD=PE时,求AP的长;
(3)设AP 的长为![]() ,四边形CDPE的面积为
,四边形CDPE的面积为![]() ,请直接写出
,请直接写出![]() 与
与![]() 的函数解析式及自变量
的函数解析式及自变量![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,![]() ACB=90°,DE是AB边的垂直平分线,与AC交于点D,与AB交于点E,M是BD的中点
ACB=90°,DE是AB边的垂直平分线,与AC交于点D,与AB交于点E,M是BD的中点
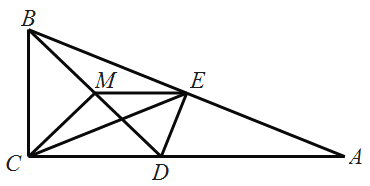
(1)求证: CM= EM;
(2)当线段AC长度改变时, △CME与△ABD的面积之比是否发生变化?如果不变,求出比值;如果发生变化。说明如何变化.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).

(1)图2中的阴影部分的面积为 ;
(2)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若x+y=7,xy=![]() ,则x﹣y= ;
,则x﹣y= ;
(4)实际上通过计算图形的面积可以探求相应的等式.根据图3,写出一个因式分解的等式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点A(0,6)的直线AB与直线OC相交于点C(2,4)动点P沿路线O→C→B运动.(1)求直线AB的解析式;(2)当△OPB的面积是△OBC的面积的![]() 时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.
时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与证明:

如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.
(1)连接AE,求证:△AEF是等腰三角形;
猜想与发现:
(2)在(1)的条件下,请判断线段MD与MN的关系,得出结论;
结论:DM、MN的关系是: ;
拓展与探究:
(3)如图2,将图1中的直角三角板ECF绕点C旋转180°,其他条件不变,则(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=![]() ,求CD的长.
,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AB=CD,E,F分别为边BC与AD的中点,AE∥CD,延长BA,CD,分别与EF的延长线交于点G,H,连接AH,ED.
(1)求证:AH∥ED;
(2)求证:AE=AG.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com