练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在四边形ABCD中，AB=CD，E，F分别为边BC与AD的中点，AE∥CD，延长BA，CD，分别与EF的延长线交于点G，H，连接AH，ED.

    （1）求证：AH∥ED；

    （2）求证：AE=AG.

    【答案】（1）（2）见解析.

    【解析】

    （1）证△AEF≌△DHF. 得AE=DH.由AE∥DH，得四边形AEDH是平行四边形.（2）连接AC，设AC的中点为O，连接OE，OF.根据三角形中位线性质得OF∥CD，OF=CD，OE∥AB，OE=AB，OE=OF. 得∠OFE=∠OEF，∠DHE =∠AGE. 由AE∥DH，得∠DHE =∠AEG. 所以∠AGE =∠AEG.

    （1）∵AE∥CD，

    ∴∠AEF=∠DHF，∠FAE=∠FDH.

    ∵AF=FD，

    ∴△AEF≌△DHF.

    ∴AE=DH.

    ∵AE∥DH，

    ∴四边形AEDH是平行四边形.

    ∴AH∥ED.

    （2）连接AC，设AC的中点为O，连接OE，OF.

    ∵E，F分别为边BC与AD的中点，

    ∴OF∥CD，OF=CD，OE∥AB，OE=AB.

    ∴∠OFE=∠DHE，∠OEF=∠AGE.

    ∵AB=CD，

    ∴OE=OF.

    ∴∠OFE=∠OEF.

    ∴∠DHE =∠AGE.

    ∵AE∥DH，

    ∴∠DHE =∠AEG.

    ∴∠AGE =∠AEG.

    ∴AE=AG.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

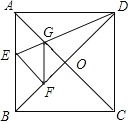
    【题目】如图，正方形ABCD中，对角线AC、BD交于点O，折叠正方形纸片，使AD落在BC上，点A恰好与BD上的点F重合，展开后折痕DE分别交AB，AC于点E、G，连结GF，给出下列结论①∠AGD＝110.5°；②S△AGD＝S△OGD；③四边形AEFG是菱形；④BF＝OF；⑤如果S△OGF＝1，那么正方形ABCD的面积是12+8，其中正确的有（　　）个．

    A.2个B.3个C.4个D.5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（12分）某工厂生产一种产品，当产量至少为10吨，但不超过55吨时，每吨的成本（万元/吨）与产量（吨）之间是一次函数关系，函数与自变量的部分对应值如下表：

    （吨）

    10

    20

    30

    （万元/吨）

    45

    40

    35

    （1）求与的函数关系式，并写出自变量的取值范围；

    （2）当投入生产这种产品的总成本为1200万元时，求该产品的总产量；（注：总成本=每吨成本×总产量）

    （3）市场调查发现，这种产品每月销售量（吨）与销售单价（万元/吨）之间满足如图所示的函数关系．该厂第一个月按同一销售单价卖出这种产品25吨，请求出该厂第一个月销售这种产品获得的利润．（注：利润=售价—成本）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABD≌△CDB，且AB，CD是对应边．下面四个结论中不正确的是( )

    A. △ABD和△CDB的面积相等B. △ABD和△CDB的周长相等

    C. ∠A+∠ABD=∠C+∠CBDD. AD∥BC，且AD=BC

    查看答案和解析>>

    科目：初中数学 来源： 题型：

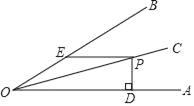
    【题目】已知OC平分∠AOB，点P为OC上一点，PD⊥OA于D，且PD=3cm，过点P作PE∥OA交OB于E，∠AOB=30°，求PE的长度_____cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC三个顶点坐标分别为A（﹣3，﹣1），B（﹣4，﹣4），C（﹣1，﹣2），结合所给平面直角坐标系解答下列问题：

    （1）将△ABC向右平移5个单位长度，再向上平移6个单位，画出平移后的△A1B1C1．

    （2）将△ABC绕原点O顺时针旋转90°，画出旋转后的△A2B2C2，此时点A2的坐标为_____．

    （3）若以A、B、C、D为顶点的四边形是平行四边形，请直接满足条件的点D的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，∠BAC=540，以AB为直径的⊙O分别交AC，BC于点D，E，过点B作⊙O的切线，交AC的延长线于点F。

    （1）求证：BE=CE；

    （2）求∠CBF的度数；

    （3）若AB=6，求的长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点M（n，﹣n ）在第二象限，过点M的直线y=kx+b（0＜k＜1）分别交x轴、y轴于点A，B，过点M作MN⊥x轴于点N，则下列点在线段AN的是（　　）

    A. （（k﹣1）n，0） B. （（k+）n，0）） C. （，0） D. （（k+1）n，0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系，跨度AB=44米，∠A=45°，AC1=4米，点D2的坐标为(-13，-1.69)，则桥架的拱高OH=________米.

    查看答案和解析>>

    同步练习册答案