
【题目】如图,在△ABC中,![]() ACB=90°,DE是AB边的垂直平分线,与AC交于点D,与AB交于点E,M是BD的中点
ACB=90°,DE是AB边的垂直平分线,与AC交于点D,与AB交于点E,M是BD的中点
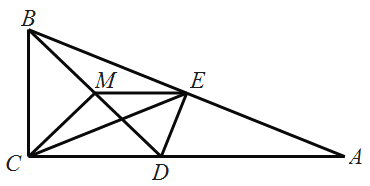
(1)求证: CM= EM;
(2)当线段AC长度改变时, △CME与△ABD的面积之比是否发生变化?如果不变,求出比值;如果发生变化。说明如何变化.
【答案】(1)见解析(2)△CME与△ABD的面积之比=1:4,理由见解析.
【解析】
(1)利用三角形的中位线定理条件直角三角形斜边中线的性质即可解决问题.
(2)结论:△CME与△ABD的面积之比=1:4.利用相似三角形的性质即可解决问题.
(1)证明:∵DE是AB边的垂直平分线,
∴AE=BE,DB=AD,
∵BM=MD,
∴EM=![]() AD,
AD,
∵∠BCD=90°,BM=MD,
∴CM=![]() BD,
BD,
∴CM=EM.
(2)解:结论:△CME与△ABD的面积之比=1:4.
理由:∵DE垂直平分线段AB,
∴DB=DA,∵MC=ME,
∴△MCE,△ADB都是等腰三角形,
∵EM∥AC,
∴∠MEC=∠ECA,
∵∠ACB=90°,BE=EA,
∴∠ECA=∠A,
∴∠MEC=∠A,
∴△MEC∽△DAB,
∴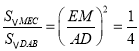 .
.


科目:初中数学 来源: 题型:
【题目】注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路,填写表格,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填写表格, 只需按照解答题的一般要求,进行解答即可.
某校八年级学生由距博物馆 10km 的学校出发前往参观,一部分同学骑自行车先走,过了20min 后,其余同学乘汽车出发,结果他们同时到达.已知汽车的速度是骑车同学速度 的 2 倍,求骑车同学的速度.
设骑车同学的速度为 xkm / h
(Ⅰ)根据题意,利用速度、时间、路程之间的关系,用含有 x 的式子填写下表:
速度(千米 / 时) | 所用时间(时 ) | 所走的路程(千米) | |
骑自行车 | x | 10 | |
乘汽车 | 10 |
(Ⅱ)列出方程,并求出问题的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,等腰直角三角形ABC中,∠BAC=90°,BA=AC,点E、F是线段BC上两动点且∠EAF=45°,请写出BE、EF、FC之间的等量关系并证明.
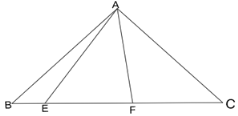
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了全面提升中小学教师的综合素质,贵阳市将对教师的专业知识每三年进行一次考核.某校决定为全校数学教师每人购买一本义务教育《数学课程标准(2011年版)》(以下简称《标准》),同时每人配套购买一本《数学课程标准(2011年版)解读》(以下简称《解读》),其中《解读》的单价比《标准》的单价多25元.若学校购买《标准》用了378元,购买《解读》用了1053元,请问《标准》和《解读》的单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习“分式”一章后,老师写出下面的一道题让同学们解答.
计算:![]() 其中小明的解答过程如下:
其中小明的解答过程如下:
解:原式 (A)
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
(1)上述计算过程中,是从哪一步开始出现错误的?请写出该步代号:______;
(2)写出错误原因是____________;
(3)本题正确的解答过程.
解:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,对角线AC、BD交于点O,折叠正方形纸片,使AD落在BC上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB,AC于点E、G,连结GF,给出下列结论①∠AGD=110.5°;②S△AGD=S△OGD;③四边形AEFG是菱形;④BF=![]() OF;⑤如果S△OGF=1,那么正方形ABCD的面积是12+8
OF;⑤如果S△OGF=1,那么正方形ABCD的面积是12+8![]() ,其中正确的有( )个.
,其中正确的有( )个.
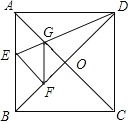
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABD≌△CDB,且AB,CD是对应边.下面四个结论中不正确的是( )

A. △ABD和△CDB的面积相等B. △ABD和△CDB的周长相等
C. ∠A+∠ABD=∠C+∠CBDD. AD∥BC,且AD=BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com