
【题目】注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路,填写表格,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填写表格, 只需按照解答题的一般要求,进行解答即可.
某校八年级学生由距博物馆 10km 的学校出发前往参观,一部分同学骑自行车先走,过了20min 后,其余同学乘汽车出发,结果他们同时到达.已知汽车的速度是骑车同学速度 的 2 倍,求骑车同学的速度.
设骑车同学的速度为 xkm / h
(Ⅰ)根据题意,利用速度、时间、路程之间的关系,用含有 x 的式子填写下表:
速度(千米 / 时) | 所用时间(时 ) | 所走的路程(千米) | |
骑自行车 | x | 10 | |
乘汽车 | 10 |
(Ⅱ)列出方程,并求出问题的解.
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=![]() ,AD=1.
,AD=1.
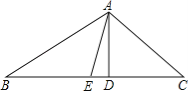
(1)求BC的长;
(2)求tan∠DAE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
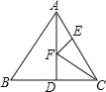
【题目】等边△ABC 的边长为 4,AD 是 BC 边上的中线,F 是边 AD 上的动点,E 是边 AC 上的点, 当 AE=2,且 EF+CF 取得最小值时.
(Ⅰ)能否求出∠ECF 的度数?_____(用“能”或“否”填空);
(Ⅱ)如果能,请你在图中作出点 F(保留作图痕迹,不写证明).并直接写出∠ECF 的度 数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2-2ax+c与x轴交于A,B两点,与y轴正半轴交于点C,且A(-1,0).
(1)一元二次方程ax2-2ax+c=0的解是 ;
(2)一元二次不等式ax2-2ax+c>0的解集是 ;
(3)若抛物线的顶点在直线y=2x上,求此抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC=6![]() ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )

A. 6 B. 3![]() C. 2
C. 2![]() D. 4.5
D. 4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC为弦,∠BAC的平分线交⊙O于点D,过点D的切线交AC的延长线于点G.
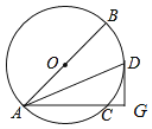
求证:(1)DG⊥AG;
(2)AG+CG=AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,![]() ACB=90°,DE是AB边的垂直平分线,与AC交于点D,与AB交于点E,M是BD的中点
ACB=90°,DE是AB边的垂直平分线,与AC交于点D,与AB交于点E,M是BD的中点
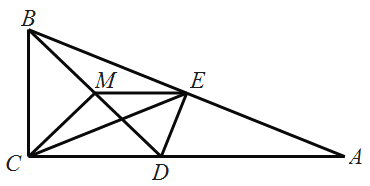
(1)求证: CM= EM;
(2)当线段AC长度改变时, △CME与△ABD的面积之比是否发生变化?如果不变,求出比值;如果发生变化。说明如何变化.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com