
【题目】如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB中点,在“①DE=AC;②DE⊥AC;③∠EAF=∠ADE;④∠CAB=30°”这四个结论中,正确的个数有 ( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
根据点D是AB的中点,得到AD=![]() ,由于AB=2BC,于是得到AD=BC,证得Rt△AED≌Rt△BAC,得到∠E=∠CAB,DE=AC,故①正确;由∠E+∠EDA=90°,得到∠FAD+∠EDA=90°,即可得到DE⊥AC,故②正确;根据同角的余角相等得到∠EAF=∠ADE,故③正确;根据BC是AB的一半,而不是AC的一半,故∠CAB不等于30°,故④错误.
,由于AB=2BC,于是得到AD=BC,证得Rt△AED≌Rt△BAC,得到∠E=∠CAB,DE=AC,故①正确;由∠E+∠EDA=90°,得到∠FAD+∠EDA=90°,即可得到DE⊥AC,故②正确;根据同角的余角相等得到∠EAF=∠ADE,故③正确;根据BC是AB的一半,而不是AC的一半,故∠CAB不等于30°,故④错误.
解:
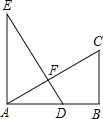
点D是AB的中点,则AD=![]() ,
,
∵AB=2BC,
∴AD=BC,
∵EA⊥AB,CB⊥AB,
∴∠B=∠EAB=90°,
在△AED与△BAC中, ,
,
∴△AED≌△BAC,
∴∠E=∠CAB,DE=AC,
∴①正确;
∵∠E+∠EDA=90°,
∴∠FAD+∠EDA=90°,
∴∠AFD=180°-(∠FAD+∠EDA)=90°,
∴DE⊥AC,
∴②正确;
∵∠EAF与∠ADE都是∠E的余角,
∴∠EAF=∠ADE,
∴③正确;
∵BC是AB的一半,而不是AC的一半,故∠CAB不等于30°,
∴④错误;
故选:C.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
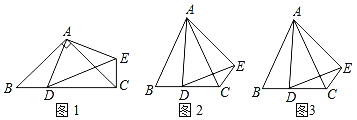
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=_____度;如图2,当点D在线段BC上,如果∠BAC=60°,则∠BCE=______度.
(2)设∠BAC=α,∠BCE=β,如图3,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州市处于东南沿海,夏季经常遭受台风袭击,一次,温州气象局测得台风中心在温州市![]() 的正西方向300千米的
的正西方向300千米的![]() 处,以每小时
处,以每小时![]() 千米的速度向东偏南
千米的速度向东偏南![]() 的
的![]() 方向移动,距台风中心200千米的范围是受台风严重影响的区域,试问:
方向移动,距台风中心200千米的范围是受台风严重影响的区域,试问:
(1)台风中心在移动过程中离温州市最近距离是多少千米?
(2)温州市![]() 是否受台风影响?若不会受到,请说明理由;若会受到,求出温州市受台风严重影响的时间.
是否受台风影响?若不会受到,请说明理由;若会受到,求出温州市受台风严重影响的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:等边△ABC中,点E为△ABC内一点.
(1)如图1,联结AE、BE并延长分别与BC、CA边交于点D、F。如果∠AEB=120°,求证:△ABD![]() △BCF。
△BCF。
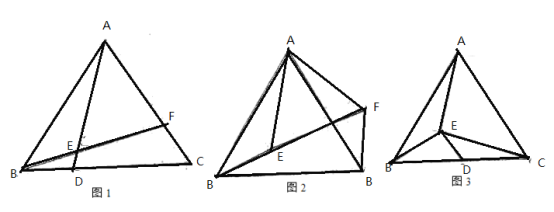
(2)如图2、以AE为一边作等边△AEF,联结BE、CF,求证:BE=CF.
(3)如图3、点D为BC的中点,联结BE、CE,若∠BEC=120°,联结AE、DE,求证:AE=2DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB=4,点P是AB边上一个动点,过点P作AB的垂线交AC边与点D,以PD为边作∠DPE=60°,PE交BC边与点E.
(1)当点D为AC边的中点时,求BE的长;
(2)当PD=PE时,求AP的长;
(3)设AP 的长为![]() ,四边形CDPE的面积为
,四边形CDPE的面积为![]() ,请直接写出
,请直接写出![]() 与
与![]() 的函数解析式及自变量
的函数解析式及自变量![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面对话:
小红妈:“售货员,请帮我买些梨.”
售货员:“小红妈,您上次买的那种梨都卖完了,我们还没来得及进货,我建议这次您买些进的苹果,价格比梨贵一点,不过苹果的营养价值更高.”
小红妈:“好,你们很讲信用,这次我照上次一样,也花30元钱。”对照前后两次的电脑小票,小红妈发现:每千克苹果的价是梨的1.5倍,苹果的重量比梨轻2.5千克.
试根据上面对话和小红妈的发现,分别求出梨和苹果的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).

(1)图2中的阴影部分的面积为 ;
(2)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若x+y=7,xy=![]() ,则x﹣y= ;
,则x﹣y= ;
(4)实际上通过计算图形的面积可以探求相应的等式.根据图3,写出一个因式分解的等式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,地震、泥石流等自然灾害频繁发生,造成极大的生命和财产损失.为了更好地做好“防震减灾”工作,我市相关部门对某中学学生“防震减灾”的知晓率采取随机抽样的方法进行问卷调查,调查结果分为“非常了解”、“比较了解”、“基本了解”和“不了解”四个等级.小明根据调查结果绘制了如图1、2的统计图,请根据提供的信息回答问题:
(1)本次调查中,样本容量是________;
(2)扇形统计图中“基本了解”部分所对应的扇形圆心角是________;在该校2000名学生中随机提问一名学生,对“防震减灾”不了解的概率的估计值为________;
(3)请在图2中补全频数分布直方图.

图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com