
【题目】已知:等边△ABC中,点E为△ABC内一点.
(1)如图1,联结AE、BE并延长分别与BC、CA边交于点D、F。如果∠AEB=120°,求证:△ABD![]() △BCF。
△BCF。
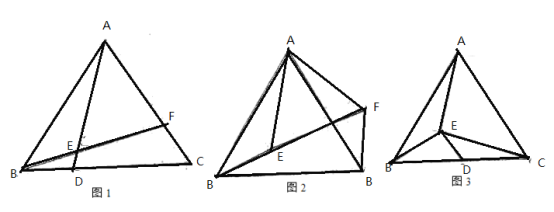
(2)如图2、以AE为一边作等边△AEF,联结BE、CF,求证:BE=CF.
(3)如图3、点D为BC的中点,联结BE、CE,若∠BEC=120°,联结AE、DE,求证:AE=2DE.
【答案】(1)见详解;(2)见详解;(3)见详解.
【解析】
(1)由∠AEB=120°,得到∠BAE+∠ABE=60°,即可得到∠BAE=∠CBF,然后利用ASA证明△ABD≌△BCF即可;
(2)由等边三角形△ABC、△AEF,得到AB=AC,AE=AF,∠BAC=∠EAF=60°,则得到∠BAE=∠CAF,然后证明△ABE≌△ACF,即可得到结论成立;
(3)把△ABE逆时针旋转60°,得到△ACF,连接EF,延长ED至点G,使得ED=DG,连接CG. 由旋转的性质,得△ABE≌△ACF,且△AEF时等边三角形;由∠BEC=120°,得到∠EBD+∠ECD=60°,根据角的等量代换得到∠ECF=∠ECG=60°,然后得到△ECG≌△ECF,得到EG=EF=AE,即可得到AE=2ED.
证明:(1)如图,
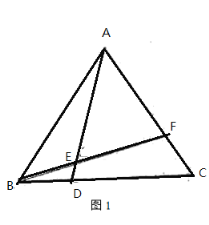
在等边△ABC中,有AB=BC,∠ABC=∠C=60°,
∵∠AEB=120°,
∴∠BED=180°![]() 120°=60°,
120°=60°,
∴∠BAE+∠ABE=60°,
∵∠CBF+∠ABE=∠ABC=60°,
∴∠BAE=∠CBF,
∴△ABD≌△BCF(ASA);
(2)如图,
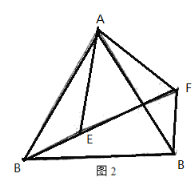
∵△ABC和△AEF是等边三角形,
∴AB=AC,AE=AF,∠BAC=∠EAF=60°,
∴∠BAE+∠EAC=∠EAC+∠CAF=60°,
∴∠BAE=∠CAF,
∴△ABE≌△ACF(SAS),
∴BE=CF;
(3)如图,把△ABE逆时针旋转60°,得到△ACF,连接EF,延长ED至点G,使得ED=DG,连接CG.
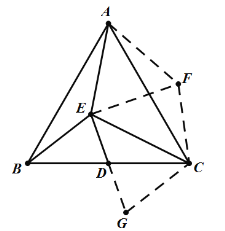
由旋转的性质,得:△ABE≌△ACF,且△AEF时等边三角形,
∴AE=AF=EF,BE=CF,∠ABE=∠ACF,
∵∠BEC=120°,
∴∠EBD+∠ECD=60°,
∵∠EBD+∠ABE=∠ABC=60°,
∴∠ABE=∠ECD=∠ACF,
∴∠ACF+∠ACE=∠ECD+∠ACE=∠ACB=60°,
∴∠ECF=60°.
∵ED=DG,∠BDE=∠CDG,BD=CD,
∴△BDE≌△CDG,
∴BE=CG=CF,∠EBD=GCD,
∴∠GCD+∠ECD=∠EBD+∠ABE=∠ABC=60°,
∴∠ECG=60°,
∴∠ECF=∠ECG=60°,
在△ECG和△ECF中,
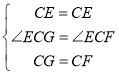 ,
,
∴△ECG≌△ECF,
∴EG=EF=AE,
∵EG=2ED,
∴AE=2ED.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
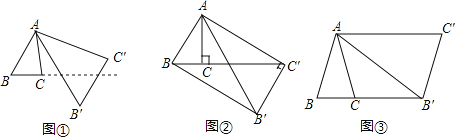
(1)如图①,对△ABC作变换[60°,![]() ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l为y=![]() x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(_______).
x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(_______).

查看答案和解析>>
科目:初中数学 来源: 题型:
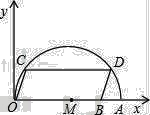
【题目】如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边与点E,连接AD,若AE=4cm,则△ABD的周长是( )

A. 22cmB. 20cmC. 18cmD. 15cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB中点,在“①DE=AC;②DE⊥AC;③∠EAF=∠ADE;④∠CAB=30°”这四个结论中,正确的个数有 ( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果二次函数![]() 的图象与
的图象与![]() 轴有两个公共点,那么一元二次方程
轴有两个公共点,那么一元二次方程![]() 有两个不相等的实根,请根据你对这句话的理解,解决下列问题:若
有两个不相等的实根,请根据你对这句话的理解,解决下列问题:若![]() 、
、![]() (
(![]() <
<![]() )是关于的方程
)是关于的方程![]() 的两根,且
的两根,且![]() <
<![]() 则
则![]() 、
、![]() 、
、![]() 、
、![]() 的大小关系是( )
的大小关系是( )
A. ![]() <
<![]() <
<![]() <
<![]() B.
B. ![]() <
<![]() <
<![]() <
<![]()
C. ![]() <
<![]() <
<![]() <
<![]() D.
D. ![]() <
<![]() <
<![]() <
<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,![]() ,点
,点![]() 为
为![]() 内一点,
内一点,![]() ,
,![]() 分别是点
分别是点![]() 关于
关于![]() 、
、![]() 的对称点,连接
的对称点,连接![]() ,分别交
,分别交![]() 于
于![]() 、
、![]() 于
于![]() .如果
.如果![]() ,
,![]() 的周长为
的周长为![]() ,
,![]() 的度数为
的度数为![]() ,请根据以上信息完成作图,并指出
,请根据以上信息完成作图,并指出![]() 和
和![]() 的值( )
的值( )

A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图,在Rt△ABC中,∠ACB=90°∠BAC=30°.
动手操作:(1)若以直角边AC所在的直线为对称轴.将Rt△ABC作轴对称变换,请你在原图上作出它的对称图形:
观察发现:(2)Rt△ABC和它的对称图形组成了什么图形?你最准确的判断是 .
合作交流:(3)根据上面的图形,请你猜想直角边BC与斜边AB的数量关系,并证明你的猜想.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com