
ĄŸÌâÄżĄżÔÚŐę·œĐÎABCDÖĐŁŹÁŹœÓBDŁź
Łš1Ł©ÈçÍŒ1ŁŹAEĄÍBDÓÚEŁźÖ±œÓĐŽłöĄÏBAE”ĶÈÊ꣟
Łš2Ł©ÈçÍŒ1ŁŹÔÚŁš1Ł©”ÄÌőŒțÏÂŁŹœ«ĄśAEBÒÔAĐęŚȘÖĐĐÄŁŹŃŰÄæʱŐë·œÏòĐęŚȘ30Ąășó”Ă”œĄśABĄäEĄäŁŹABĄäÓëBDœ»ÓÚMŁŹAEĄä”ÄŃÓł€ÏßÓëBDœ»ÓÚNŁź


ąÙÒÀÌâÒâČčÈ«ÍŒ1Ł»
ąÚÓĂ”ÈÊœ±íÊŸÏ߶ÎBMĄąDNșÍMNÖźŒä”ÄÊęÁżčŰÏ”ŁŹČąÖ€ĂśŁź
Łš3Ł©ÈçÍŒ2ŁŹEĄąFÊDZßBCĄąCDÉÏ”Ä”ăŁŹĄśCEFÖÜł€ÊÇŐę·œĐÎABCDÖÜł€”ÄÒ»°ëŁŹAEĄąAF·Ö±đÓëBDœ»ÓÚMĄąNŁŹĐŽłöĆжÏÏ߶ÎBMĄąDNĄąMNÖźŒäÊęÁżčŰÏ””Äˌ·ŁźŁšČ»±ŰĐŽłöÍêŐûÍÆÀíčęłÌŁ©
ĄŸŽđ°žĄżŁš1Ł©ĄÏBAE”ĶÈÊęÎȘ45ĄăŁ»Łš2Ł©ąÙČčÈ«ÍŒŒûœâÎöŁ»ąÚBMĄąDNșÍMNÖźŒä”ÄÊęÁżčŰÏ”ÊÇBM2+MD2=MN2ŁŹÀíÓÉŒûœâÎöŁ»Łš3Ł©ËŒÂ·ŒûœâÎö.
ĄŸœâÎöĄżŁš1Ł©ÀûÓĂ”ÈŃüÖ±œÇÈęœÇĐΔÄĐÔÖÊŒŽżÉŁ»
Łš2Ł©ÒÀÌâÒ⻳öÈçÍŒ1ËùÊŸ”ÄÍŒĐÎŁŹžùŸĘĐÔÖÊșÍŐę·œĐΔÄĐÔÖÊŁŹĆжÏÏ߶ΔÄčŰÏ”ŁŹÔÙÀûÓĂčŽčɶšÀí”Ă”œFB2+BM2=FM2ŁŹÔÙĆĐ¶ÏłöFM=MNŒŽżÉŁ»
Łš3Ł©ÀûÓĂĄśCEFÖÜł€ÊÇŐę·œĐÎABCDÖÜł€”ÄÒ»°ëŁŹĆĐ¶ÏłöEF=EGŁŹÔÙÀûÓĂŁš2Ł©Ö€ĂśŒŽżÉŁź
œâŁșŁš1Ł©ĄßBDÊÇŐę·œĐÎABCD”ĶԜÇÏߣŹĄàĄÏABD=ĄÏADB=45ĄăŁŹ
ĄßAEĄÍBDŁŹĄàĄÏABE=ĄÏBAE=45ĄăŁŹ
Łš2Ł©ąÙÒÀÌâÒâČčÈ«ÍŒĐÎŁŹÈçÍŒ1ËùÊŸŁŹ
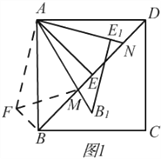
ąÚBMĄąDNșÍMNÖźŒä”ÄÊęÁżčŰÏ”ÊÇBM2+MD2=MN2ŁŹ
œ«ĄśANDÈÆ”ăDËłÊ±ŐëĐęŚȘ90ĄăŁŹ”Ă”œĄśAFBŁŹ
ĄàĄÏADB=ĄÏFBAŁŹĄÏBAF=ĄÏDANŁŹDN=BFŁŹAF=ANŁŹ
ĄßÔÚŐę·œĐÎABCDÖĐŁŹAEĄÍBDŁŹĄàĄÏADB=ĄÏABD=45ĄăŁŹ
ĄàĄÏFBM=ĄÏFBA+ĄÏABD=ĄÏADB+ĄÏABD=90ĄăŁŹ
ÔÚRtĄśBFMÖĐŁŹžùŸĘčŽčɶšÀí”ĂŁŹFB2+BM2=FM2ŁŹ
ĄßĐęŚȘĄśANE”Ă”œAB1E1ŁŹĄàĄÏE1AB1=45ĄăŁŹĄàĄÏBAB1+ĄÏDAN=90Ąă©45Ąă=45ĄăŁŹ
ĄßĄÏBAF=DANŁŹĄàĄÏBAB1+ĄÏBAF=45ĄăŁŹĄàĄÏFAM=45ĄăŁŹĄàĄÏFAM=ĄÏE1AB1ŁŹ
ĄßAM=AMŁŹAF=ANŁŹĄàĄśAFMĄŐĄśANMŁŹĄàFM=MNŁŹ
ĄßFB2+BM2=FM2ŁŹĄàDN2+BM2=MN2ŁŹ
Łš3Ł©ÈçÍŒ2ŁŹ
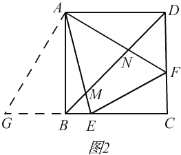
œ«ĄśADFÈÆ”ăAËłÊ±ŐëĐęŚȘ90Ąă”Ă”œĄśABGŁŹĄàDF=GBŁŹ
ĄßŐę·œĐÎABCD”ÄÖÜł€ÎȘ4ABŁŹĄśCEFÖÜł€ÎȘEF+EC+CFŁŹ
ĄßĄśCEFÖÜł€ÊÇŐę·œĐÎABCDÖÜł€”ÄÒ»°ëŁŹĄà4AB=2ŁšEF+EC+CFŁ©ŁŹĄà2AB=EF+EC+CF
ĄßEC=AB©BEŁŹCF=AB©DFŁŹĄà2AB=EF+AB©BE+AB©DFŁŹĄàEF=DF+BEŁŹ
ĄßDF=GBŁŹĄàEF=GB+BE=GEŁŹÓÉĐęŚȘ”Ă”œAD=AG=ABŁŹ
ĄßAM=AMŁŹĄàĄśAEGĄŐĄśAEFŁŹĄÏEAG=ĄÏEAF=45ĄăŁŹșÍŁš2Ł©”ÄąÚÒ»ŃùŁŹ”Ă”œDN2+BM2=MN2Łź
Ą°”ăŸŠĄ±ŽËÌâÊÇËıßĐÎŚÛșÏÌ⣏֜ÒȘżŒČéÁËŐę·œĐΔÄĐÔÖÊĄąĐęŚȘ”ÄĐÔÖÊŁŹÈęœÇĐΔÄÈ«”ÈŁŹĆĐ¶ÏłöŁšĄśAFNĄŐĄśANMŁŹ”Ă”œFM=MMŁ©ŁŹÊÇœâÌâ”ÄčŰŒü.


 łćŽÌ100·Ö1șĆŸíÏ”ÁĐŽđ°ž
łćŽÌ100·Ö1șĆŸíÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÏÂÁĐÊÂŒțÊDZŰÈ»ÊÂŒț”ÄÊÇ( )
A.ĂśÌìÊÇÇçÌì
B.ÓĐһƄÂí”ıŒĆÜËÙ¶ÈÊÇ100ĂŚ/Ăë
C.ŽòżȘ”çÊÓŐęÔÚČ„čăžæ
D.ÔÚ”ŰĂæÉÏÏòżŐÖĐĆŚÖÀÒ»ÊŻżéŁŹÊŻżéÖŐœ«ÂäÏÂ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżŸĘÏôÉœÇűÀͶŻ±ŁŐÏŸÖÍłŒÆŁŹ”œĄ°ÊźÒ»Î楱ĩŁŹÈ«ÇűÀÛŒÆČΌӞśÀàŃűÀϱŁÏŐŚÜÈËÊęŽï”œ88.2ÍòÈËŁŹ±ÈĄ°ÊźÎ楱ĩÔöŒÓ37.7ÍòÈËŁŹČΌӞśÀàÒœÁƱŁÏŐŚÜÈËÊęŽï”œ130.5ÍòÈËŁŹœ«ÊęŸĘ130.5ÍòÓĂżÆѧŒÇÊę·šŁšŸ«È·”œÊźÍòλŁ©±íÊŸÎȘŁš Ł©
A.1.3ĄÁ102
B.1.305ĄÁ106
C.1.3ĄÁ106
D.1.3ĄÁ105
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈô”„ÏîÊœ2x2yaŁ«bÓëŁ3xa-by4ÊÇÍŹÀàÏÔòËüĂǔĻęÎȘ_____________
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈôÒ»žöœÇ”ÄČčœÇÊÇŐâžöœÇ”ÄÓàœÇ”Ä4±¶ŁŹÔòŐâžöœÇ”ĶÈÊęÎȘ________.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒËùÊŸŁŹËıßĐÎABCDÖĐŁŹ¶ÔœÇÏßACŁŹBDÏàœ»ÓÚ”ăOŁŹÏÂÁĐĆжÏÖĐŁŹČ»ÄÜĆжÏËıßĐÎABCDÊÇŸŰĐΔÄÊÇŁš Ł© 
A.AB=CDŁŹAD=BCŁŹĄÏBAD=90Ąă
B.OA=OB=OC=OD
C.ABĄÎCDÇÒAB=CDŁŹAC=BD
D.ABĄÎCDÇÒAB=CDŁŹOA=OCŁŹOB=OD
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈôŸŰĐΔÄÒ»žöÄڜǔÄÆœ·ÖÏß°ŃŸŰĐΔÄÒ»Ìő±ß·ÖłÉ3cmșÍ5cm”ÄÁœ¶ÎŁŹÔòžĂŸŰĐΔÄÖÜł€ÎȘ Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚABCDÖĐŁŹAE=CGŁŹBF=DHŁŹÁŹœÓEFŁŹFGŁŹGHŁŹHEŁźÇóÖ€ŁșËıßĐÎEFGHÊÇÆœĐĐËıßĐÎŁź 
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄż2019Äê4ÔÂ17ÈŐŁŹčúŒÒÍłŒÆŸÖč«ČŒ2019ÄêÒ»ŒŸ¶ÈÖĐčúŸŒĂÊęŸĘŁźłőČœșËËăŁŹÒ»ŒŸ¶ÈčúÄÚÉúČúŚÜÖ”213433ÒÚÔȘŁŹ°ŽżÉ±ÈŒÛžńŒÆË㣏͏±ÈÔöł€6.4%ŁźÊęŸĘ213433ÒÚÓĂżÆѧŒÇÊę·š±íÊŸÓŠÎȘŁšĄĄĄĄŁ©
A.2.13433ĄÁ1013B.0.213433ĄÁ1014
C.213.433ĄÁ1012D.2.13433ĄÁ1014
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com