
【题目】如图,正方形OABC与正方形ODEF是位似图形,O为位似中心,相似比为1: ![]() ,点A的坐标为(1,0),则E点的坐标为( )
,点A的坐标为(1,0),则E点的坐标为( ) 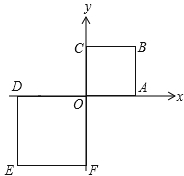
A.(- ![]() ,0)
,0)
B.(-1.5,-1.5)
C.(- ![]() ,-
,- ![]() )
)
D.(-2,-2)
科目:初中数学 来源: 题型:
【题目】在《九章算术》中有求三角形面积公式“底乘高的一半”,但是在实际丈量土地面积时,量出高并非易事,所以古人想到了能否利用三角形的三条边长来求面积.我国南宋著名的数学家秦九韶(![]() 年—
年—![]() 年)提出了“三斜求积术”,阐述了利用三角形三边长求三角形面积方法,简称秦九韶公式.在海伦(公元
年)提出了“三斜求积术”,阐述了利用三角形三边长求三角形面积方法,简称秦九韶公式.在海伦(公元![]() 年左右,生平不详)的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法,相传这个公式最早是由古希腊数学家阿基米德(公元前
年左右,生平不详)的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法,相传这个公式最早是由古希腊数学家阿基米德(公元前![]() 年—公元前
年—公元前![]() 年)得出的,故我国称这个公式为海伦一秦九韶公式.它的表达为:三角形三边长分别为
年)得出的,故我国称这个公式为海伦一秦九韶公式.它的表达为:三角形三边长分别为![]() 、
、![]() 、
、![]() ,则三角形的面积
,则三角形的面积![]() (公式里的
(公式里的![]() 为半周长即周长的一半).
为半周长即周长的一半).
请利用海伦一秦九韶公式解决以下问题:
(![]() )三边长分别为
)三边长分别为![]() 、
、![]() 、
、![]() 的三角形面积为__________.
的三角形面积为__________.
(![]() )四边形
)四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 的面积为__________.
的面积为__________.
(![]() )五边形
)五边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,五边形
,五边形![]() 的面积为__________.
的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当x>0时,反比例函数 ![]() ( )
( )
A.图象在第四象限,y随x的增大而增大
B.图象在第三象限,y随x的增大而增大
C.图象在第二象限,y随x的增大而减小
D.图象在第一象限,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组,某天乘一辆汽车检修东西走向的“汉施公路”时,约定向东行驶为正,向西行驶为负,他们从A地出发到收工时的行走记录为(单位:千米):-4,+7,-9,+8,+6,-5,+10,-8.
(1)收工时,该小组距离A地多远?
(2) 若汽车行驶每千米耗油0.2升,那么从A地出发到回到A地共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试判断∠PED的度数,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
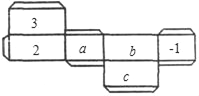
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空: a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下: 甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )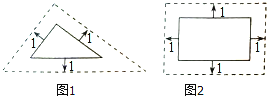
A.两人都对
B.两人都不对
C.甲对,乙不对
D.甲不对,乙对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com