
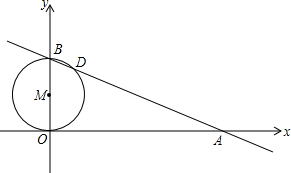
 如图,直线y=-
如图,直线y=-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| OB |
| OA |
| 4 | ||
4
|
| ||
| 3 |
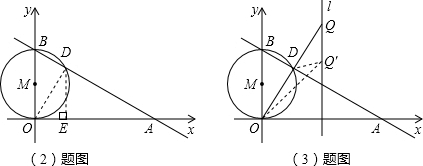 ,
,| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
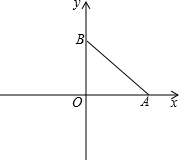 如图,在平面直角坐标系中,A、B两点的坐标分别为A(4,0),B(0,3).
如图,在平面直角坐标系中,A、B两点的坐标分别为A(4,0),B(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.查看答案和解析>>
科目:初中数学 来源: 题型:
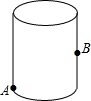 没有上盖的圆柱盒高为10cm,底面周长为32cm,点A距离下底面3cm.一只位于圆柱盒外表面点A处的蚂蚁想爬到盒内表面对侧中点B处.则蚂蚁需要爬行的最短路程的长为
没有上盖的圆柱盒高为10cm,底面周长为32cm,点A距离下底面3cm.一只位于圆柱盒外表面点A处的蚂蚁想爬到盒内表面对侧中点B处.则蚂蚁需要爬行的最短路程的长为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com