
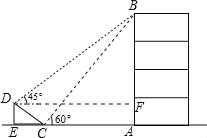
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)

【答案】(1)2米;(2)(6+)或(6-)米.
【解析】
试题分析:(1)在在Rt△DCE中,利用30°所对直角边等于斜边的一半,可求出DE=2米;(2)过点D作DF⊥AB于点F,则AF=2,根据三角函数可用BF表示BC、BD,然后可判断△BCD是Rt△,进而利用勾股定理可求得BF的长,AB的高度也可求.
试题解析:(1)在Rt△DCE中,∠DEC=90°,∠DCE=30°,∴DE=DC=2米;(2)过D作DF⊥AB,交AB于点F,则AF=DE=2米.∵∠BFD=90°,∠BDF=45°,∴∠BFD=45°,∴BF=DF.设BF=DF=x米,则AB=(x+2)米,在Rt△ABC中,∠BAC=90°,∠BCA=60°,∴sin∠BCA=,∴BC=AB÷sin∠BCA=(x+2)÷![]() =
=![]() 米,在Rt△BDF中,∠BFD=90°,
米,在Rt△BDF中,∠BFD=90°,![]() 米,∵∠DCE=30°,∠ACB=60°,∴∠DCB=90°.∴
米,∵∠DCE=30°,∠ACB=60°,∴∠DCB=90°.∴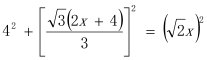 ,解得:x=4+或x=4﹣,则AB=(6+)米或(6﹣)米.
,解得:x=4+或x=4﹣,则AB=(6+)米或(6﹣)米.


科目:初中数学 来源: 题型:
【题目】已知四边形ABCD中,AB=AD,AB⊥AD,连接AC,过点A作AE⊥AC,且使AE=AC,连接BE,过A作AH⊥CD于H交BE于F.
(1)如图1,当E在CD的延长线上时,求证:①△ABC≌△ADE;②BF=EF;
(2)如图2,当E不在CD的延长线上时,BF=EF还成立吗?请证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,最适合采用全面调查的是( )
A.对一锅汤的味道进行调查B.对某班全体学生出生日期的调查
C.对某批次灯泡使用寿命的调查D.对全国中学生每天阅读时间的调查
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com