
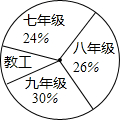
 某校组织开展“迎新春长跑活动”,将报名的男运动员共分成4组,分别是:七年级组、八年级组、九年级组、教工组,各组人数所占比例如图所示,已知九年级组有60人,则教工组人数是40.
某校组织开展“迎新春长跑活动”,将报名的男运动员共分成4组,分别是:七年级组、八年级组、九年级组、教工组,各组人数所占比例如图所示,已知九年级组有60人,则教工组人数是40. 科目:初中数学 来源: 题型:填空题
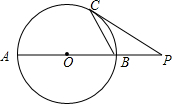 如图,C是⊙O上的一点,过点C的⊙O的切线交直径AB的延长线于点P,若OB=PB=2$\sqrt{3}$,则BC的长为2$\sqrt{3}$.
如图,C是⊙O上的一点,过点C的⊙O的切线交直径AB的延长线于点P,若OB=PB=2$\sqrt{3}$,则BC的长为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
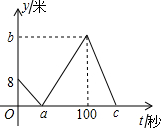 小明和小亮在操场的同一条笔直的跑道上进行500米匀速跑步训练,他们从同一地点出发,先到达终点的人原地休息,已知小明先出发2秒,在跑步的过程中,小明和小亮的距离y(米)与小亮出发的时间t(秒)之间的函数关系如图所示,下列四种说法:
小明和小亮在操场的同一条笔直的跑道上进行500米匀速跑步训练,他们从同一地点出发,先到达终点的人原地休息,已知小明先出发2秒,在跑步的过程中,小明和小亮的距离y(米)与小亮出发的时间t(秒)之间的函数关系如图所示,下列四种说法:| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
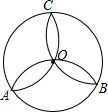 如图,在A处有两只蚂蚁,一只从A出发,沿圆过B,C回到A,另一只则从A到O,到B,再从另一条线回到O,到C,再沿圆(不过B)回到A.如果两只蚂蚁爬得一样快,哪只蚂蚁先回到A处?为什么?
如图,在A处有两只蚂蚁,一只从A出发,沿圆过B,C回到A,另一只则从A到O,到B,再从另一条线回到O,到C,再沿圆(不过B)回到A.如果两只蚂蚁爬得一样快,哪只蚂蚁先回到A处?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
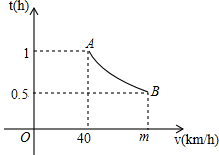 某段公路经测算发现,匀速行驶的车辆通过该段公路时,所需时间t(h)与行驶速度v(km/h)满足反比例函数关系,其图象为如图所示的一段曲线.且端点为A(40,1)和B(m,0.5).
某段公路经测算发现,匀速行驶的车辆通过该段公路时,所需时间t(h)与行驶速度v(km/h)满足反比例函数关系,其图象为如图所示的一段曲线.且端点为A(40,1)和B(m,0.5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
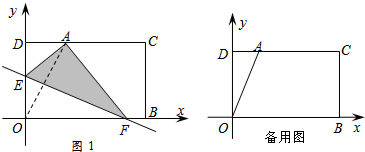
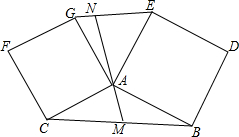 如图,四边形ABDE和ACFG都是正方形,过A作直线l,交BC,GE于M、N.
如图,四边形ABDE和ACFG都是正方形,过A作直线l,交BC,GE于M、N.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{-2}$ | B. | $\sqrt{0.03}$ | C. | $\sqrt{x}$ | D. | $\sqrt{-{x}^{2}-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
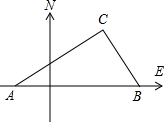 如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,乙巡逻艇的航向为北偏西40°.
如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,乙巡逻艇的航向为北偏西40°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com