
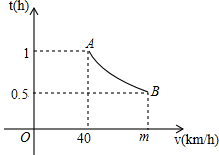
 某段公路经测算发现,匀速行驶的车辆通过该段公路时,所需时间t(h)与行驶速度v(km/h)满足反比例函数关系,其图象为如图所示的一段曲线.且端点为A(40,1)和B(m,0.5).
某段公路经测算发现,匀速行驶的车辆通过该段公路时,所需时间t(h)与行驶速度v(km/h)满足反比例函数关系,其图象为如图所示的一段曲线.且端点为A(40,1)和B(m,0.5).分析 (1)设t与v的函数关系式为t=$\frac{k}{v}$(k≠0),把A的坐标代入解析式,利用待定系数法求得函数解析式,然后把B(m,0.5)代入解析式求得m的值;
(2)求得当v=50时t的值,根据图象即可作出解答.
解答 解:(1)由题意,可设t与v的函数关系式为t=$\frac{k}{v}$(k≠0),
∵函数t=$\frac{k}{v}$经过点A(40,1),
∴1=$\frac{k}{40}$,解得k=40,
∴t与v的函数关系式为t=$\frac{40}{v}$;
把B(m,0.5)代入t=$\frac{40}{v}$,
得0.5=$\frac{40}{m}$,解得m=80;
(2)把v=50代入t=$\frac{40}{v}$,得t=$\frac{40}{50}$=0.8,
则通过该路段需要的最短时间是0.8小时,这段公路的长为40km.
点评 本题考查了反比例函数的实际应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
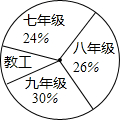 某校组织开展“迎新春长跑活动”,将报名的男运动员共分成4组,分别是:七年级组、八年级组、九年级组、教工组,各组人数所占比例如图所示,已知九年级组有60人,则教工组人数是40.
某校组织开展“迎新春长跑活动”,将报名的男运动员共分成4组,分别是:七年级组、八年级组、九年级组、教工组,各组人数所占比例如图所示,已知九年级组有60人,则教工组人数是40.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
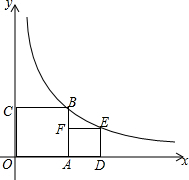 如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{4}{x}$(x>0)的图象上,则点E的坐标是($\sqrt{5}$+1,$\sqrt{5}$-1)
如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{4}{x}$(x>0)的图象上,则点E的坐标是($\sqrt{5}$+1,$\sqrt{5}$-1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
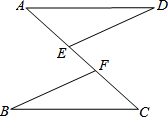 已知:如图,E,F在AC上,AD∥CB且AD=CB,∠D=∠B.
已知:如图,E,F在AC上,AD∥CB且AD=CB,∠D=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com