
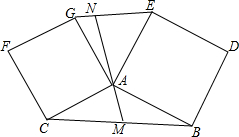
 如图,四边形ABDE和ACFG都是正方形,过A作直线l,交BC,GE于M、N.
如图,四边形ABDE和ACFG都是正方形,过A作直线l,交BC,GE于M、N.分析 (1)作KG∥AC交AM的延长线于K,连接CK,先证明△ACM≌△KBM,再证明∠EAG≌△BAK得∠AGE=∠AKB=∠CAK,根据∠GAN+∠CAK=90°即可解决问题.
(2)作KG∥AC交AM的延长线于K,连接CK,先证明△EAG≌△BAK,证明四边形ACKB是平行四边形即可.
解答 (1)证明:作KG∥AC交AM的延长线于K,连接CK.
∵AC∥BK,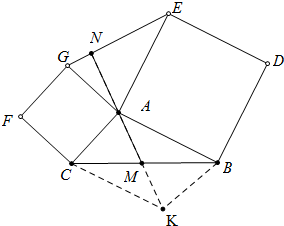
∴∠ACM=∠MBG,
在△ACM和△KBM中,
$\left\{\begin{array}{l}{∠ACM=∠MBK}\\{∠AMC=∠BMK}\\{CM=BM}\end{array}\right.$,
∴△ACM≌△KBM,
∴AC=BK,
∴四边形ACKB是平行四边形,
∴∠CAB+∠ABK=180°,AC=BK,
∵∠EAG+∠CAB=180°,
∴∠EAG=∠ABK,
∵四边形ACFG、ABDE是正方形,
∴AC=AG,AB=AE,∠CAG=90°,
在△AEG和△BAK中,
$\left\{\begin{array}{l}{AG=BK}\\{∠EAG=∠ABK}\\{AE=AB}\end{array}\right.$
∴∠EAG≌△BAK,
∴∠AGE=∠AKB,
∵∠AKB=∠CAK,
∠CAK+∠GAN=90°,
∴∠AGN+∠GAN=90°,
∴∠ANG=90°即AN⊥EG.
(2)作KG∥AC交AM的延长线于K,连接CK.
∵AN⊥EG,
∴∠ANG=90°,∠AGE+∠GAN=90°,
∵∠GAN+∠CAK=90°,
∴∠AGN=∠CAK,
∵∠CAK=∠AKB,
∴∠AGE=∠AKB,
在△EAG和△BAK中,
$\left\{\begin{array}{l}{∠AGE=∠AKB}\\{∠EAG=∠ABK}\\{AE=AB}\end{array}\right.$,
∴△EAG≌△BAK,
∴AG=BK=AC,
∴四边形ACKB是平行四边形,
∴CM=BM.
点评 本题考查全等三角形的判定和性质、正方形的性质等知识,解题的关键是正确寻找全等三角形,学会添加辅助线构造全等三角形以及特殊四边形,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
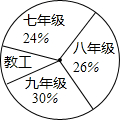 某校组织开展“迎新春长跑活动”,将报名的男运动员共分成4组,分别是:七年级组、八年级组、九年级组、教工组,各组人数所占比例如图所示,已知九年级组有60人,则教工组人数是40.
某校组织开展“迎新春长跑活动”,将报名的男运动员共分成4组,分别是:七年级组、八年级组、九年级组、教工组,各组人数所占比例如图所示,已知九年级组有60人,则教工组人数是40.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
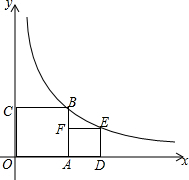 如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{4}{x}$(x>0)的图象上,则点E的坐标是($\sqrt{5}$+1,$\sqrt{5}$-1)
如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{4}{x}$(x>0)的图象上,则点E的坐标是($\sqrt{5}$+1,$\sqrt{5}$-1)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com