
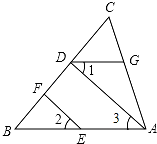
 已知:∠CGD=∠CAB,∠1=∠2,AD⊥BC,求证:EF⊥BC.
已知:∠CGD=∠CAB,∠1=∠2,AD⊥BC,求证:EF⊥BC. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
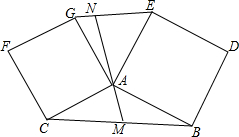 如图,四边形ABDE和ACFG都是正方形,过A作直线l,交BC,GE于M、N.
如图,四边形ABDE和ACFG都是正方形,过A作直线l,交BC,GE于M、N.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{-2}$ | B. | $\sqrt{0.03}$ | C. | $\sqrt{x}$ | D. | $\sqrt{-{x}^{2}-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{3^2}$ | B. | $\sqrt{-{3^2}}$ | C. | $\sqrt{{{({-3})}^2}}$ | D. | $\sqrt{|{-3}|}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
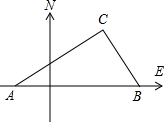 如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,乙巡逻艇的航向为北偏西40°.
如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,乙巡逻艇的航向为北偏西40°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com