
| x(万元) | 1 | 2 | 2.5 | 3 | 5 |
| yA(万元) | 0.4 | 0.8 | 1 | 1.2 | 2 |
分析 (1)根据表格中对应的关系可以确定为一次函数,通过待定系数法求得函数表达式;
(2)用待定系数法将坐标(2,2.4),(4,3.2)代入函数关系式yB=ax2+bx求解即可;
(3)根据等量关系“总利润=投资A产品所获利润+投资B产品所获利润”列出函数关系式求得最大值.
解答 解:(1)根据表格中对应的关系可以确定为一次函数,
故设函数关系式yA=kx+b,将(1,0.4)(2,0.8)代入得:
$\left\{\begin{array}{l}{k+b=0.4}\\{2k+b=0.8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=0.4}\\{b=0}\end{array}\right.$.
则yA=0.4x;
(2)由题意得,将坐标(2,2.4)(4,3.2)代入函数关系式yB=ax2+bx,
$\left\{\begin{array}{l}{4a+2b=2.4}\\{16a+4b=3.2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-0.2}\\{b=1.6}\end{array}\right.$.
故yB与x的函数关系式:yB=-0.2x2+1.6x,
当yB=3时,-0.2x2+1.6x=3,解得x1=3,x2=5.
故利润yB为3(万元)应投资金额为3万元或5万元;
(3)设投资B产品x万元,投资A产品(15-x)万元,总利润为W万元,
W=-0.2x2+1.6x+0.4(15-x)=-0.2(x-3)2+7.8,
即当投资B3万元,A12万元时所获总利润最大,为7.8万元.
点评 本题主要考查了二次函数和一次函数的实际应用,运用待定系数法求出函数关系式以及根据二次函数的性质确定最大值是解决问题的关键.


科目:初中数学 来源: 题型:解答题
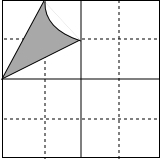 如图,已知网格中每个小正方形的边长为都是1,图中的阴影部分图案是一条以格点为圆心,以1为半径的圆弧和两条线段围成.
如图,已知网格中每个小正方形的边长为都是1,图中的阴影部分图案是一条以格点为圆心,以1为半径的圆弧和两条线段围成.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
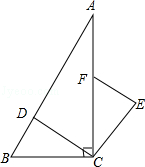 如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.62×102 | B. | 16.2×10 | C. | 1.62×106 | D. | 1.62×105 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com