
| 甲 | 10 | 9 | 8 | 5 | 8 |
| 乙 | 8 | 8 | 7 | 9 | 8 |
| A. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,${s_甲}^2$>${s_乙}^2$ | B. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${s_甲}^2$<${s_乙}^2$ | ||
| C. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${s_甲}^2={s_乙}^2$ | D. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${s_甲}^2$>${s_乙}^2$ |
分析 分别计算平均数和方差后比较即可得到答案.
解答 解:(1)$\overline{{x}_{甲}}$=$\frac{1}{5}$(10+8+9+8+10)=9;
$\overline{{x}_{乙}}$=$\frac{1}{5}$(9+8+9+10+9)=9;
${s_甲}^2$=$\frac{1}{5}$[(10-9)2+(8-9)2+(9-9)2+(8-9)2+(10-9)2]=0.8;
${s_乙}^2$=$\frac{1}{5}$[(9-9)2+(8-9)2+(9-9)2+(10-9)2+(9-9)2]=0.4;
∴$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${s_甲}^2$>${s_乙}^2$.
故选D.
点评 本题考查了方差,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:解答题
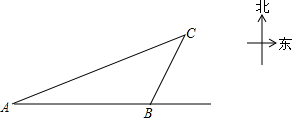 一艘轮船自西向东航行,在A处测得北偏东68.7°方向有一座小岛C,继续向东航行22海里到达B处,测得小岛C此时在轮船的北偏东26.5°方向上,而小岛C方圆10海里的范围内有暗礁,轮船继续向东航行有无触礁的危险呢?请说明理由.(参考数据:sin21.3°≈$\frac{9}{25}$,tan21.3°≈$\frac{2}{5}$,sin63.5°≈$\frac{9}{10}$,tan63.5°≈2)
一艘轮船自西向东航行,在A处测得北偏东68.7°方向有一座小岛C,继续向东航行22海里到达B处,测得小岛C此时在轮船的北偏东26.5°方向上,而小岛C方圆10海里的范围内有暗礁,轮船继续向东航行有无触礁的危险呢?请说明理由.(参考数据:sin21.3°≈$\frac{9}{25}$,tan21.3°≈$\frac{2}{5}$,sin63.5°≈$\frac{9}{10}$,tan63.5°≈2)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>-$\frac{a}{2}$ | B. | x>-$\frac{a}{3}$ | C. | x>$\frac{a}{3}$ | D. | x>$\frac{a}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知函数y=2x和函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4.
如图,已知函数y=2x和函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
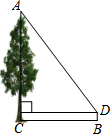 如图,B为地面上一点,测得点B到树底部C的距离为10米,在点B处放置一个1米高的测角仪BD,并测得树顶A的仰角为53°,则树高AC约为14.3 米(精确到0.1米).
如图,B为地面上一点,测得点B到树底部C的距离为10米,在点B处放置一个1米高的测角仪BD,并测得树顶A的仰角为53°,则树高AC约为14.3 米(精确到0.1米).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com