
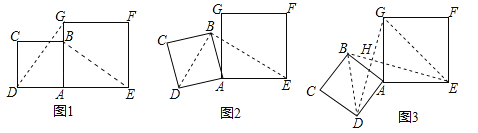
【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为![]() 的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
(1)小明发现DG⊥BE,请你帮他说明理由;
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长;
(3)如图3,小明将正方形ABCD绕点A继续逆时针旋转,线段DG与线段BE将相交,交点为H,写出△GHE与△BHD面积之和的最大值,并简要说明理由.
【答案】(1)理由见试题解析;(2)![]() ;(3)6.
;(3)6.
【解析】
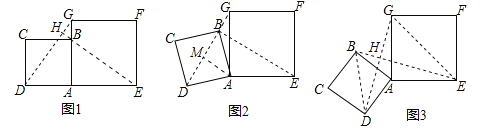
试题分析:(1)由四边形ABCD与四边形AEFG为正方形,利用正方形的性质得到两对边相等,且夹角相等,利用SAS得到三角形ADG与三角形ABE全等,利用全等三角形对应角相等得∠AGD=∠AEB,如图1所示,延长EB交DG于点H,利用等角的余角相等得到∠DHE=90°,利用垂直的定义即可得DG⊥BE;
(2)由四边形ABCD与四边形AEFG为正方形,利用正方形的性质得到两对边相等,且夹角相等,利用SAS得到三角形ADG与三角形ABE全等,利用全等三角形对应边相等得到DG=BE,如图2,过点A作AM⊥DG交DG于点M,∠AMD=∠AMG=90°,在直角三角形AMD中,求出AM的长,即为DM的长,根据勾股定理求出GM的长,进而确定出DG的长,即为BE的长;
(3)△GHE和△BHD面积之和的最大值为6,理由为:对于△EGH,点H在以EG为直径的圆上,即当点H与点A重合时,△EGH的高最大;对于△BDH,点H在以BD为直径的圆上,即当点H与点A重合时,△BDH的高最大,即可确定出面积的最大值.
试题解析:(1)∵四边形ABCD和四边形AEFG都为正方形,∴AD=AB,∠DAG=∠BAE=90°,AG=AE,在△ADG和△ABE中,∵AD=AB, ∠DAG=∠BAE=90°,AG=AE,∴△ADG≌△ABE(SAS),∴∠AGD=∠AEB,如图1所示,延长EB交DG于点H,在△ADG中,∠AGD+∠ADG=90°,∴∠AEB+∠ADG=90°,在△EDH中,∠AEB+∠ADG+∠DHE=180°,∴∠DHE=90°,则DG⊥BE;
(2)∵四边形ABCD和四边形AEFG都为正方形,∴AD=AB,∠DAB=∠GAE=90°,AG=AE,∴∠DAB+∠BAG=∠GAE+∠BAG,即∠DAG=∠BAE,在△ADG和△ABE中,∵AD=AB, ∠DAG=∠BAE, AG=AE,∴△ADG≌△ABE(SAS),∴DG=BE,如图2,过点A作AM⊥DG交DG于点M,∠AMD=∠AMG=90°,∵BD为正方形ABCD的对角线,∴∠MDA=45°,在Rt△AMD中,∠MDA=45°,∴cos45°=![]() ,∵AD=2,∴DM=AM=
,∵AD=2,∴DM=AM=![]() ,在Rt△AMG中,根据勾股定理得:GM=
,在Rt△AMG中,根据勾股定理得:GM=![]() =
=![]() ,∵DG=DM+GM=
,∵DG=DM+GM=![]() ,∴BE=DG=
,∴BE=DG=![]() ;
;
(3)△GHE和△BHD面积之和的最大值为6,理由为:
对于△EGH,点H在以EG为直径的圆上,∴当点H与点A重合时,△EGH的高最大;
对于△BDH,点H在以BD为直径的圆上,∴当点H与点A重合时,△BDH的高最大,则△GHE和△BHD面积之和的最大值为2+4=6.


科目:初中数学 来源: 题型:
【题目】下列各数: ![]() ,3.1415,
,3.1415, ![]() ,0,
,0, ![]() ,
, ![]() ,1.3030030003……(每两个3之间多一个0)中,
,1.3030030003……(每两个3之间多一个0)中,
(1)无理数为:;
(2)整数为:;
(3)按从小到大排列,并用“<”连接.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直角三角形ABC中,∠B=90°,AB=8,BC=6,BM为中线,△BMN为等腰三角形(点N在三角形AB或AC边上,且不与顶点重合),求S△BMN .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关系式中,正确的是( )
A.(a+b)2=a2﹣2ab+b2
B.(a﹣b)2=a2﹣b2
C.(a+b)2=a2+b2
D.(a+b)(a﹣b)=a2﹣b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明同学遇到下列问题:
解方程组 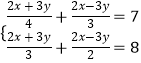 ,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:
,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:
令m=2x+3y,n=2x﹣3y.
这时原方程组化为 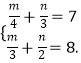 解得
解得 ![]()
把 ![]() 代入m=2x+3y,n=2x﹣3y.
代入m=2x+3y,n=2x﹣3y.
得 ![]() 解得
解得 ![]()
所以,原方程组的解为 ![]()
请你参考小明同学的做法,解决下面的问题:
(1)解方程组 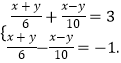
(2)若方程组 ![]() 的解是
的解是 ![]() ,求方程组
,求方程组 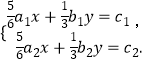 的解.
的解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com