
【题目】已知二次函数y=4x2﹣4ax+a2﹣2a+2,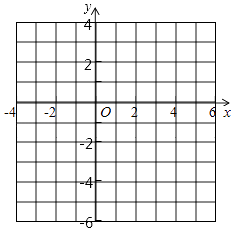
(1)当a=0,2,4时,请在同一直角坐标系中画出对应函数图象的顶点,并画出a=2 时的函数图象;
(2)证明当a取任意实数时,顶点在一条确定的直线上;
(3)求(2)中的直线被抛物线y=4x2﹣4ax+a2﹣2a+2截得的线段长.
【答案】
(1)解:∵二次函数y=4x2﹣4ax+a2﹣2a+2=4(x﹣ ![]() a)2﹣2a+2,
a)2﹣2a+2,
∴抛物线的顶点坐标为( ![]() a,﹣2a+2).
a,﹣2a+2).
当a=0时,抛物线的顶点坐标为(0,2);
当a=2时,抛物线的顶点坐标为(1,﹣2),抛物线的解析式为y=4(x﹣1)2﹣2;
当a=4时,抛物线的顶点坐标为(2,﹣6).
画出函数图象如图所示
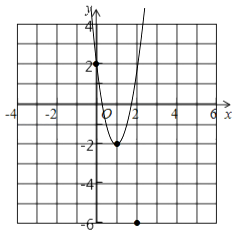
(2)证明:∵抛物线的顶点坐标为( ![]() a,﹣2a+2),
a,﹣2a+2),
∴﹣2a+2=﹣4×( ![]() a)+2,
a)+2,
∴y=﹣4x+2,即当a取任意实数时,顶点在一条确定的直线上
(3)解:联立两函数解析式成方程组,
![]() ,解得:
,解得: 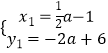 ,
, 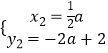 ,
,
∴两函数的交点坐标为( ![]() a﹣1,﹣2a+6),(
a﹣1,﹣2a+6),( ![]() a,﹣2a+2),
a,﹣2a+2),
∴(2)中的直线被抛物线y=4x2﹣4ax+a2﹣2a+2截得的线段长为 ![]() =
= ![]()
【解析】(1) 利用配方法将二次函数解析式由一般式变形为顶点式,由此可得出抛物线的顶点坐标,分别代入a=0、a=2、a=4找出顶点坐标,并画出a=2时,二次函数的图象即可;
(2)由待定系数法,将抛物线的顶点坐标代入直线的解析式,消去a后即可得出y=-4x+2,此题得证;
(3)联立两函数解析式成方程组,通过解方程组求出交点坐标,再根据两点间的距离公式求出线段长度即可.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
①abc>0;②b<a+c;③4a﹣2b+c>0;④2c<3b;⑤当m≤x≤m+1时,函数的最大值为a+b+c,则0≤m≤1;
其中正确的结论有( )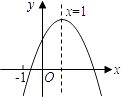
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】供电局的电力维修工要到30千米远的郊区进行电力抢修.技术工人骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果他们同时到达.已知抢修车的速度是摩托车的1.5倍,求这两种车的速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】基本事实:“若ab=0,则a=0或b=0”.一元二次方程x2-x-2=0可通过因式分解化为(x-2)(x+1)=0,由基本事实得x-2=0或x+1=0,即方程的解为x=2或x=-1.
(1)、试利用上述基本事实,解方程:2x2-x=0:
(2)、若(x2+y2)(x2+y2-1)-2=0,求x2+y2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.
(1)求证:AE是⊙O的切线;
(2)已知AE=8cm,CD=12cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮利用三张卡片做游戏,卡片上分别写有A,B,B.这些卡片除字母外完全相同,从中随机摸出一张,记下字母后放回,充分洗匀后,再从中摸出一张,如果两次摸到卡片字母相同则小明胜,否则小亮胜,这个游戏对双方公平吗?请说明现由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com