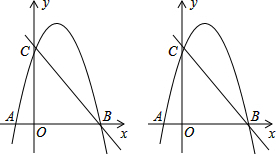˝â´đŁş˝âŁşŁ¨1Ł©Éč¶ţ´ÎşŻĘýµÄ˝âÎöʽΪy=ax
2+cx+dŁ¬
Ôň
Ł¬
˝âµĂŁş
Ł¬
ˇŕ¶ţ´ÎşŻĘýµÄ˝âÎöʽΪŁşy=
Ł¨x-2Ł©
2=
x
2-2x+2Ł¬
ÉčÖ±ĎßABµÄ˝âÎöĘ˝µÄ˝âÎöʽΪŁşy=kx+bŁ¬
Ôň
Ł¬
˝âµĂŁş
Ł¬
ˇŕÖ±ĎßABµÄ˝âÎöĘ˝µÄ˝âÎöʽΪŁşy=x+6Ł»
Ł¨2Ł©ÉčPµă×ř±ęÎŞŁşPŁ¨xŁ¬yŁ©Ł¬ÔňQµă×ř±ęÎŞŁ¨xŁ¬
x
2-2x+2Ł©
ŇŔĚâŇâµĂŁ¬PQ=l=Ł¨x+2Ł©-
Ł¨x-2Ł©
2=-
x
2+3xŁ¬
ÓÉ
Ł¬
ÇóµĂµăBµÄ×ř±ęÎŞŁ¨6Ł¬8Ł©Ł¬

ˇŕ0ŁĽxŁĽ6Ł»
Ł¨3Ł©ÓÉŁ¨2Ł©ÖŞPµÄşá×ř±ęÎŞ0ŁĽxŁĽ6ʱŁ¬±ŘÓжÔÓ¦µÄµăQÔÚĹ×ÎďĎßÉĎŁ»
·´Ö®Ł¬QµÄşá×ř±ęÎŞ0ŁĽxŁĽ6ʱŁ¬ÔÚĎ߶ÎABÉϱŘÓĐŇ»µăPÓëÖ®¶ÔÓ¦Ł®
ĽŮÉč´ćÔÚ·űşĎĚőĽţµÄµăPŁ¬ÓÉĚâŇâµĂAMÓëPQ˛»»áĆ˝ĐĐŁ¬
Ňň´ËĚÝĐεÄÁ˝µ×Ö»ÄÜĘÇAPÓëMQŁ¬
ˇßąýµăMŁ¨2Ł¬0Ł©ÇŇĆ˝ĐĐABµÄÖ±Ďß·˝łĚÎŞy=x-2Ł¬
ÓÉÓÉ
Ł¬
ĎűČĄyµĂŁşx
2-6x+8=0Ł¬Ľ´Ł¨x-2Ł©Ł¨x-4Ł©=0Ł¬
˝âµĂx=2»ňx=4Ł¬
ˇßµ±x=2ʱŁ¬Pµăˇ˘Qµăˇ˘Mµă Čýµăą˛Ďߣ¬ÓëAµăÖ»ÄÜąąłÉČý˝ÇĐÎŁ¬¶ř˛»ÄÜąąłÉĚÝĐÎŁ»
ˇŕx=2Őâ¸ö˝âÉáČĄŁ®
ˇŕąýMµăµÄÖ±ĎßÓëĹ×ÎďĎßµÄÁíŇ»˝»µăÎŞŁ¨4Ł¬2Ł©Ł¬
ˇß´Ë˝»µăşá×ř±ę4Ł¬ÂäÔÚ0ŁĽxŁĽ6·¶Î§ÄÚŁ¬
ˇŕQµÄ×ř±ęÎŞŁ¨4Ł¬2Ł©Ę±Ł¬PŁ¨4Ł¬6Ł©·űşĎĚőĽţŁ¬
Ľ´´ćÔÚ·űşĎĚőĽţµÄµăPŁ¬Ćä×ř±ęÎŞŁ¨4Ł¬6Ł©Ł¬
ÉčÖ±ĎßABÓëxÖá˝»ÓÚNŁ¬ÓÉĚőĽţżÉÖŞŁ¬ˇ÷ANMĘǵČŃüÖ±˝ÇČý˝ÇĐÎŁ¬Ľ´AM=AN=2
Ł¬
AP=PN-AN=6
-2
=4
Ł¬MQ=2
Ł¬
AMÎŞĚÝĐÎPQMAµÄ¸ßŁ¬
ąĘS
ĚÝĐÎPQMA=
Ł¨2
+4
Ł©ˇÁ2
=12Ł®

 ČçÍĽŁ¬¶ţ´ÎşŻĘýÍĽĎóąýµăMŁ¨2Ł¬0Ł©Ł¬Ö±ĎßABÓë¸Ă¶ţ´ÎşŻĘýµÄÍĽĎó˝»ÓÚAŁ¨0Ł¬2Ł©ˇ˘BŁ¨6Ł¬8Ł©Á˝µăŁ®
ČçÍĽŁ¬¶ţ´ÎşŻĘýÍĽĎóąýµăMŁ¨2Ł¬0Ł©Ł¬Ö±ĎßABÓë¸Ă¶ţ´ÎşŻĘýµÄÍĽĎó˝»ÓÚAŁ¨0Ł¬2Ł©ˇ˘BŁ¨6Ł¬8Ł©Á˝µăŁ®



 ČçÍĽŁ¬ˇ÷ABCÖĐŁ¬AB=ACŁ¬ADˇÍBCÓÚµăDŁ¬µăEÔÚACÉĎŁ¬CE=2AEŁ¬AD=9Ł¬BE=10Ł¬ADÓëBE˝»ÓÚµăFŁ¬Ôňˇ÷ABCµÄĂć»ýĘÇ
ČçÍĽŁ¬ˇ÷ABCÖĐŁ¬AB=ACŁ¬ADˇÍBCÓÚµăDŁ¬µăEÔÚACÉĎŁ¬CE=2AEŁ¬AD=9Ł¬BE=10Ł¬ADÓëBE˝»ÓÚµăFŁ¬Ôňˇ÷ABCµÄĂć»ýĘÇ ČçÍĽŁ¬µăEˇ˘F·Ö±đÎŞŐý·˝ĐÎABCDÖĐABˇ˘BC±ßµÄÖе㣬Á¬˝ÓAFˇ˘DEĎŕ˝»ÓÚµăGŁ¬Á¬˝ÓCGŁ¬ÔňcosˇĎCGD=Ł¨ˇˇˇˇŁ©
ČçÍĽŁ¬µăEˇ˘F·Ö±đÎŞŐý·˝ĐÎABCDÖĐABˇ˘BC±ßµÄÖе㣬Á¬˝ÓAFˇ˘DEĎŕ˝»ÓÚµăGŁ¬Á¬˝ÓCGŁ¬ÔňcosˇĎCGD=Ł¨ˇˇˇˇŁ©