
科目:初中数学 来源: 题型:解答题
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 差值(kg) | -0.58 | 0.79 | 0.15 | -0.42 | 0.71 | 0.45 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对于每一个确定的x的值,y都有唯一确定的值与它相对应 | |
| B. | 只要任意给出一个x的值,就能确定y的值,所以此方程的解为任何实数 | |
| C. | 若需满足x、y都为正整数,则此方程恰有两个解 | |
| D. | 它可与二元一次方程5x-3z=2组成一个二元一次方程组 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
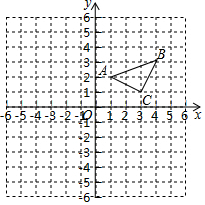 如图所示,三角形ABC三个顶点A、B、C的坐标分别为A (1,2)、B(4,3)、C(3,1).
如图所示,三角形ABC三个顶点A、B、C的坐标分别为A (1,2)、B(4,3)、C(3,1).查看答案和解析>>
科目:初中数学 来源:2017届浙江省九年级3月模拟数学试卷(解析版) 题型:解答题
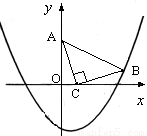
如图,在直角坐标系中,已知点A(0, 3)、点C(1, 0),等腰Rt△ACB的顶点B在抛物线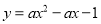 上.
上.
(1)求点B的坐标及抛物线的解析式;
(2)在抛物线上是否存在点P(点B除外),使△ACP是以AC为直角边的Rt△?若存在,求出所有点P的坐标;若不存在,请说明理由.
(3)在抛物线上是否存在点Q(点B除外),使△ACQ是以AC为直角边的等腰Rt△?若存在直接写出所有点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2017届浙江省九年级3月模拟数学试卷(解析版) 题型:填空题
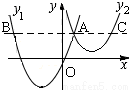
如图, 抛物线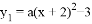 与
与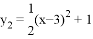 交于点A
交于点A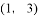 ,过点A作
,过点A作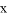 轴的平行线,分别交两条抛物线于点B、C.则以下结论:① 无论
轴的平行线,分别交两条抛物线于点B、C.则以下结论:① 无论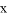 取何值,
取何值,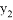 的值总是正数;②
的值总是正数;② 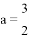 ;③ 当
;③ 当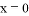 时,
时,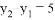 ;④ 当
;④ 当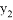 >
>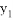 时,0≤
时,0≤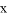 <1;⑤ 2AB=3AC.其中正确结论的编号是______________.
<1;⑤ 2AB=3AC.其中正确结论的编号是______________.
查看答案和解析>>
科目:初中数学 来源:2017届湖北省襄阳市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
如图,将正方形ABCO绕点A顺时针旋转一定角度,得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
(1)求证:△AOG≌△ADG;
(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;
(3)若正方形ABCO的边长为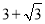 ,∠1=∠2,求AP的长.
,∠1=∠2,求AP的长.

查看答案和解析>>
科目:初中数学 来源:2017届山东省文慧学校九年级下学期第一次月考数学试卷(解析版) 题型:单选题
若关于x的一元二次方程(k-1)x₂+4x+1=0有两个不相等的实数根,则k的取值范围是( )
A. k<5 B. k<5且k≠1 C. k≤5且k≠1 D. k>5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com