练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在△ABC中，AB=AC，∠A=30°，以B为圆心，BC的长为半径圆弧，交AC于点D，连接BD，则∠ABD=（　　）

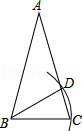
    A．  30°          B．45°          C．60°          D． 90°


    B             解：∵AB=AC，∠A=30°，

    ∴∠ABC=∠ACB=（180°﹣∠A）=（180°﹣30°）=75°，

    ∵以B为圆心，BC的长为半径圆弧，交AC于点D，

    ∴BC=BD，

    ∴∠CBD=180°﹣2∠ACB=180°﹣2×75°=30°，

    ∴∠ABD=∠ABC﹣∠CBD=75°﹣30°=45°．

    故选：B．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    方程﹣=0解是（　　）

    A．  x=          B．x=          C．x=          D． x=﹣1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某汽车销售公司经销某品牌A款汽车，随着汽车的普及，其价格也在不断下降．今年5月份A款汽车的售价比去年同期每辆降价1万元，如果卖出相同数量的A款汽车，去年销售额为100万元，今年销售额只有90万元．

    （1）今年5月份A款汽车每辆售价多少万元？

    （2）为了增加收入，汽车销售公司决定再经销同品牌的B款汽车，已知A款汽车每辆进价为7.5万元，B款汽车每辆进价为6万元，公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆，有几种进货方案？

    （3）如果B款汽车每辆售价为8万元，为打开B款汽车的销路，公司决定每售出一辆B款汽车，返还顾客现金a万元，要使（2）中所有的方案获利相同，a值应是多少？此时，哪种方案对公司更有利？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    △ABC中，已知∠A=60°，∠B=80°，则∠C的外角的度数是　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知：在△AFD和△CEB中，点A、E、F、C在同一直线上，AE=CF，∠B=∠D，AD∥BC．求证：AD=BC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知等腰三角形的两边长分別为a、b，且a、b满足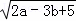+（2a+3b﹣13）2=0，则此等腰三角形的周长为（　　）

    A．  7或8          B．6或1O         C．6或7          D． 7或10

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    等腰三角形一腰上的高与另一腰的夹角为36°，则该等腰三角形的底角的度数为　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系中，A（0，4），B（2，0），点C在第一象限，若以A、B、C为顶点的三角形与△AOB相似（不包括全等），则点C的个数是（　　）

    A．  1             B．2             C．3             D． 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点P是菱形ABCD的对角线BD上一点，连接CP并延长，交AD于E，交BA的延长线点F．问：

    （1）图中△APD与哪个三角形全等？并说明理由；

    （2）求证：△APE∽△FPA；

    （3）猜想：线段PC，PE，PF之间存在什么关系？并说明理由．

    查看答案和解析>>

    同步练习册答案