
【题目】如图,四边形ABCD内接于以BC为直径的圆O,且AB=AD,延长CB、DA交于P,当PB=BO,CD=18时,求:
(1)⊙O的半径长;
(2)PA的长。
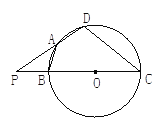
【答案】(1)12 (2)![]()
【解析】试题分析:(1)连接OA、BD交于F,由BC是 O的直径可以知道∠BDC=90°,而OA是半径,AB=AD根据垂径定理可以知道OA⊥BD,所以OA∥CD;接着可以得到![]() ;而PB=BO=OC,CD=18;现在可以求出OA了,也就求出了圆的半径.(2)由OF∥CD,OB=OC根据中位线定理可以求出OF,AF;在根据勾股定理在Rt△DBC中可以求出BD,DF;接着在Rt△ADF中求出AD;然后利用平行线的性质得∠FAD=∠CDE证明△AFD∽△DEC,利用相似三角形的对应边成比例可以求出DE了.
;而PB=BO=OC,CD=18;现在可以求出OA了,也就求出了圆的半径.(2)由OF∥CD,OB=OC根据中位线定理可以求出OF,AF;在根据勾股定理在Rt△DBC中可以求出BD,DF;接着在Rt△ADF中求出AD;然后利用平行线的性质得∠FAD=∠CDE证明△AFD∽△DEC,利用相似三角形的对应边成比例可以求出DE了.
试题解析: (1)连接OA,BD交于F,
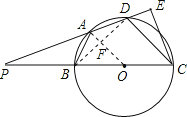
∵BC是O的直径,
∴∠BDC=90;
又∵OA是半径,AB=AD;
∴OA⊥BD,OA∥CD;
∵![]() ;
;
∴OA=12;
∴O的半径为12.
(2)∵OF∥CD, ![]() ;
;
∴OF=9,AF=3;
∵BD=![]() ;
;
∴DF= ![]() BD=
BD= ![]() ;
;
∴AD=![]()
∵OA∥CD;
∴![]() ,
,
∴AP=2AD=![]()


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】在湖边高出水面50m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°,则飞艇底部P距离湖面的高度为(参考等式: ![]() )( )
)( )
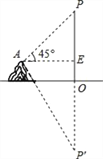
A. 25![]() +75 B. 50
+75 B. 50![]() +50 C. 75
+50 C. 75![]() +75 D. 50
+75 D. 50![]() +100
+100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则线段DE的长为( ).
A.3
B.![]()
C.5
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,a,b,c分别是ΔABC中∠A,∠B,∠C的对边,P为BC上一点,以AP为直径的圆O交AB于D,PE∥AB交AC于E,b,c是方程x2+kx+9=0的两根,且(b2+c2)(b2+c2-14)-72=0,锐角B的正弦值等于![]() 。
。
(1)求K的值;
(2)设BD=x,求四边形ADPE的面积为S关于x的函数关系式;
(3)问圆O是否能与BC相切?若能请求出x的值;若不能,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站 | A | B | C | D | E |
x(千米) | 8 | 9 | 10 | 11.5 | 13 |
y1(分钟) | 18 | 20 | 22 | 25 | 28 |
(1)求y1关于x的函数表达式;
(2)李华骑单车的时间y2(单位:分钟)也受x的影响,其关系可以用y2=![]() x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com