

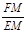 =_______;
=_______;
 角(
角( ),其他条件不变,判断
),其他条件不变,判断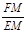 的值是否发生变化,并对你的结论进行证明;
的值是否发生变化,并对你的结论进行证明;
 ,点N在线段OD上,且NO="2." 点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.
,点N在线段OD上,且NO="2." 点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.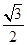 ;②不变;(2)
;②不变;(2)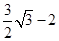 ,
,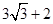
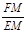 的值;②若△AOB绕点O沿顺时针方向旋转α角(0°<α<60°),其他条件不变,
的值;②若△AOB绕点O沿顺时针方向旋转α角(0°<α<60°),其他条件不变,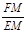 的值不发生变化,连接EF、AD、BC,由①的思路证明∠EMF=30°即可;
的值不发生变化,连接EF、AD、BC,由①的思路证明∠EMF=30°即可;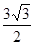 ,当旋转到OE与OD重合是,NP取最小值为:OP-ON=
,当旋转到OE与OD重合是,NP取最小值为:OP-ON=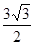 -2;当点P在点B处时,且当旋转到OB在DO的延长线时,NP取最大值OB+ON=3
-2;当点P在点B处时,且当旋转到OB在DO的延长线时,NP取最大值OB+ON=3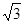 +2.
+2.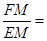
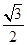 ;
; 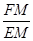 的值不变.
的值不变. 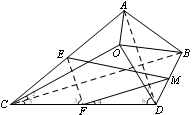
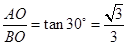
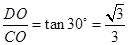 .
. 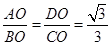
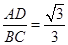 ,∠1="∠2."
,∠1="∠2." 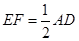 ,
,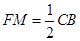
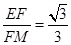 ,∠3=∠ADC=∠1+∠6,∠4="∠5."
,∠3=∠ADC=∠1+∠6,∠4="∠5." 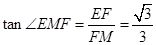 ,
,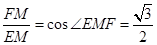 ;
;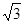 ,∠ABO=30°,
,∠ABO=30°,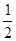 AB•OE=
AB•OE=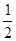 OA•OB,
OA•OB,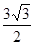 ,
,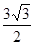 ,
,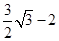 ;
;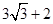 ,
,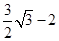 ,最大值为
,最大值为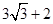 .
.

科目:初中数学 来源:不详 题型:单选题
 是方程
是方程 的解;③平行四边形既是中心对称图形又是轴对称图形;④
的解;③平行四边形既是中心对称图形又是轴对称图形;④ 的算术平方根是4。其中真命题的个数有( )
的算术平方根是4。其中真命题的个数有( )| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,AB与CE交于F,ED与AB、BC分别交于M、H.
,AB与CE交于F,ED与AB、BC分别交于M、H.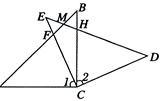
 时,试判断四边形ACDM是什么四边形?并证明你的结论.
时,试判断四边形ACDM是什么四边形?并证明你的结论.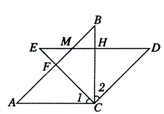
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.41º | B.149º | C.139º | D.139º或41º |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
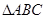 中,
中,  , 将
, 将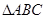 绕点
绕点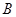 顺时针旋转角
顺时针旋转角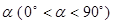 , 得
, 得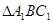 ,
, 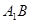 交
交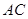 于点
于点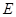 ,
,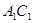 分别交
分别交 于
于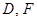 两点.
两点.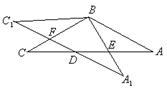
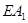 与
与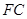 有怎样的数量关系? 证明你的结论;
有怎样的数量关系? 证明你的结论;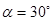 时, 试判断四边形
时, 试判断四边形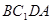 的形状, 并说明理由;
的形状, 并说明理由;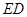 的长.
的长.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
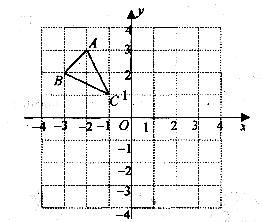
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com