
分析 (1)设甲车的速度为xkm/h,乙车的速度为ykm/h,利用路程等于时间乘以速度列方程组,然后解方程组即可;
(2)设乙车再以akm/h的速度行驶,则乙以akm/h的速度行驶的时间为(3-1)=2小时,利用甲乙行驶的路程和不小于200列不等式,然后解不等式后求出不等式的最大解即可.
解答 解:(1)设甲车的速度为xkm/h,乙车的速度为ykm/h,
根据题意得$\left\{\begin{array}{l}{2x+3y=200}\\{4x+y=200}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=40}\\{y=40}\end{array}\right.$,
答:甲车的速度为40km/h,乙车的速度为40km/h;
(2)设乙车再以akm/h的速度行驶,
根据题意得40×1+40×1+(3-1)a≥200,
解得a≥60,
答:乙车至少再以60km/h的速度行驶,才能保证在甲车出发以后3小时内与甲车相遇.
点评 本题考查了一元一次不等式的应用:由实际问题中的不等关系列出不等式,建立解决问题的数学模型,通过解不等式可以得到实际问题的答案.列不等式解应用题需要以“至少”、“最多”、“不超过”、“不低于”等词来体现问题中的不等关系.因此,建立不等式要善于从“关键词”中挖掘其内涵.也考查了二元一次方程组的应用.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 捐 款 (元) | 5 | 10 | 20 | A | 30 |
| 人 数 | 18 | 20 | B | 4 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
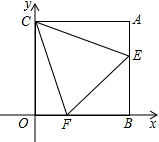 如图,在平面直角坐标系中,点A(n,m)在第一象限,AB⊥x轴于B,AC⊥y轴于C,(m-3)2+n2-6n+9=0,过C点作∠ECF分别交线段AB、OB于E、F两点.
如图,在平面直角坐标系中,点A(n,m)在第一象限,AB⊥x轴于B,AC⊥y轴于C,(m-3)2+n2-6n+9=0,过C点作∠ECF分别交线段AB、OB于E、F两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com