
【题目】探索与证明:
(1)如图①,直线![]() 经过正三角形
经过正三角形![]() 的顶点
的顶点![]() ,在直线
,在直线![]() 上取点
上取点![]() ,
,![]() ,使得
,使得![]() ,
,![]() .通过观察或测量,猜想线段
.通过观察或测量,猜想线段![]() ,
,![]() 与
与![]() 之间满足的数量关系,并予以证明;
之间满足的数量关系,并予以证明;
(2)将(1)中的直线![]() 绕着点
绕着点![]() 逆时针方向旋转一个角度到如图②的位置,
逆时针方向旋转一个角度到如图②的位置,![]() ,
,![]() .通过观察或测量,猜想线段
.通过观察或测量,猜想线段![]() ,
,![]() 与
与![]() 之间满足的数量关系,并予以证明.
之间满足的数量关系,并予以证明.
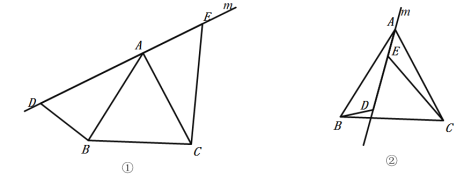
【答案】(1)DE=BD+CE,证明见解析;(2)CE =BD+DE,证明见解析
【解析】
(1)根据等边三角形的性质可得AB=CA,∠BAC=60°,然后根据已知条件可得![]() ,并且可证出∠ABD=∠CAE,利用AAS即可证出△ABD≌△CAE,从而得出BD=AE,AD= CE,然后根据DE=AE+AD和等量代换即可得出结论;
,并且可证出∠ABD=∠CAE,利用AAS即可证出△ABD≌△CAE,从而得出BD=AE,AD= CE,然后根据DE=AE+AD和等量代换即可得出结论;
(2)根据等边三角形的性质可得AB=CA,∠BAC=60°,然后根据已知条件可得![]() ,并且可证出∠ABD=∠CAE,利用AAS即可证出△ABD≌△CAE,从而得出BD=AE,AD= CE,然后根据AD= AE+DE和等量代换即可得出结论;
,并且可证出∠ABD=∠CAE,利用AAS即可证出△ABD≌△CAE,从而得出BD=AE,AD= CE,然后根据AD= AE+DE和等量代换即可得出结论;
解:(1)DE=BD+CE,证明如下
∵△ABC为等边三角形
∴AB=CA,∠BAC=60°
∵![]() ,
,![]()
∴![]()
∴∠ABD+∠BAD=180°-∠ADB=120°
∠CAE+∠BAD=180°-∠BAC=120°
∴∠ABD=∠CAE
在△ABD和△CAE中
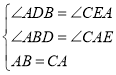
∴△ABD≌△CAE
∴BD=AE,AD= CE
∴DE=AE+AD= BD+CE;
(2)CE =BD+DE,证明如下
∵△ABC为等边三角形
∴AB=CA,∠BAC=60°
∵![]() ,
,![]()
∴![]()
∴∠ABD+∠BAD=180°-∠ADB=60°
∠CAE+∠BAD=∠BAC=60°
∴∠ABD=∠CAE
在△ABD和△CAE中
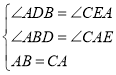
∴△ABD≌△CAE
∴BD=AE,AD= CE
∵AD= AE+DE
∴CE= BD+DE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B与∠C的角平分线相交于点I,过点I作BC的平行线,分别交AB、AC于点D、E.若AB=9,AC=6,BC=8,则△ADE的周长是( )
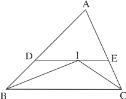
A. 14B. 15C. 17D. 23
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若四边形的一条对角线把四边形分成两个等腰三角形,则这条对角线叫做这个四边形的“巧分线”,这个四边形叫“巧妙四边形”,若一个四边形有两条巧分线,则称为“绝妙四边形”.
(1)下列四边形一定是巧妙四边形的是 ;(填序号点①平行四边形;②矩形;③菱形;④正方形.
初步应用
(2)在绝妙四边形ABCD中,AC垂直平分BD,若∠BAD=80°,则∠BCD= ;
深入研究
(3)如图,在梯形ABCD中,AD∥BC,AB=AD=CD,∠B=72°.求证:梯形ABCD是绝妙四边形.
(4)在巧妙四边形ABCD中,AB=AD=CD,∠A=90°,AC是四边形ABCD的巧分线,请直接写出∠BCD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中的箭头所示方向运动,第一次从原点运动到点(2,2)第2次运动到点A(4,0),第3次接着运动到点(6,1)……按这样的运动规律,经过第2018次运动后动点P的坐标是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分6分)
(1)(3分)(-3)2-|-![]() |+(3.14-x)0
|+(3.14-x)0
(2)(4分)先化简,再求值:[(2x-y)2+(2x-y)(2x+y)]÷(4x),其中x=2,y=-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读下文,寻找规律:
已知 x≠1 时,(1-x)(1+x)=1-x![]() ,
,
(1-x)(1+x+x![]() )=1-x
)=1-x![]() ,
,
(1-x)(1+x+x![]() +x
+x![]() )=1-x
)=1-x![]() .…
.…
观察上式,并猜想:
(1-x)(1+x+x![]() + x
+ x![]() +x
+x![]() )= ____________. (1-x)(1+x+x
)= ____________. (1-x)(1+x+x![]() +…+x
+…+x![]() )= ____________.
)= ____________.
(2) 通过以上规律,请你进行下面的探素:
①(a-b)(a+b)= ____________.
②(a-b)(a![]() +ab+b
+ab+b![]() )= ____________.
)= ____________.
③(a-b)(a![]() +a
+a![]() +ab
+ab![]() +b
+b![]() )= ____________.
)= ____________.
(3) 根据你的猜想,计算:
1+2+2![]() +…+2
+…+2![]() +2
+2![]() +2
+2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数 |
第1组 |
| 6 |
第2组 |
| 8 |
第3组 |
| 14 |
第4组 |
| a |
第5组 |
| 10 |
请结合图表完成下列各题
![]() 求表中a的值;
求表中a的值;![]() 频数分布直方图补充完整;
频数分布直方图补充完整;
![]() 小亮想根据此直方图绘制一个扇形统计图,请你帮他算出成绩为
小亮想根据此直方图绘制一个扇形统计图,请你帮他算出成绩为![]() 这一组所对应的扇形的圆心角的度数;
这一组所对应的扇形的圆心角的度数;
![]() 若测试成绩不低于80分为优秀,则本次测试的优秀率
若测试成绩不低于80分为优秀,则本次测试的优秀率![]() 百分比
百分比![]() 是多少?
是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com