
【题目】如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=﹣1,下列结论中: ①ab>0,②a+b+c>0,③当﹣2<x<0时,y<0.
正确的个数是( )
A.0个
B.1个
C.2个
D.3个
【答案】D
【解析】解:①∵抛物线的开口向上, ∴a>0,
∵对称轴在y轴的左侧,
∴b>0
∴ab>0;故①正确;②∵观察图象知;当x=1时y=a+b+c>0,
∴②正确;③∵抛物线的对称轴为x=﹣1,与x轴交于(0,0),
∴另一个交点为(﹣2,0),
∴当﹣2<x<0时,y<0;故③正确;
故选D.
【考点精析】本题主要考查了二次函数图象以及系数a、b、c的关系的相关知识点,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究1:如图l,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90![]() +
+![]() ∠A,理由如下:
∠A,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线
∴∠1=![]() ∠ABC, ∠2=
∠ABC, ∠2=![]() ∠ACB
∠ACB
∴∠l+∠2=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180
(180![]() -∠A)= 90
-∠A)= 90![]() -
-![]() ∠A
∠A
∴∠BOC=180![]() -(∠1+∠2) =180
-(∠1+∠2) =180![]() -(90
-(90![]() -
-![]() ∠A)=90
∠A)=90![]() +
+![]() ∠A
∠A
(1)探究2;如图2中,O是![]() ∠ABC与外角
∠ABC与外角![]() ∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
(2)探究3:如图3中, O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(直接写出结论)
(3)拓展:如图4,在四边形ABCD中,O是∠ABC与∠DCB的平分线BO和CO的交点,则∠BOC与∠A+∠D有怎样的关系?(直接写出结论)

查看答案和解析>>
科目:初中数学 来源: 题型:
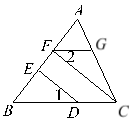
【题目】如图∠1=∠2,CF⊥AB,DE⊥AB,求证:FG∥BC.
证明:∵CF⊥AB,DE⊥AB (已知)
∴∠BED=90°,∠BFC=90°( )
∴∠BED=∠BFC ( )
∴ED∥FC ( )
∴∠1=∠BCF ( )
∵∠2=∠1 ( 已知 )
∴∠2=∠BCF ( )
∴FG∥BC ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列等式:①由a=b,得5﹣2a=5﹣2b;②由a=b,得ac=bc;③由a=b,得![]() ;④由
;④由![]() ,得3a=2b;
,得3a=2b;
⑤由a2=b2,得a=b.其中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式ax5+bx3+3x+c,当x=0时,该代数式的值为﹣1.
(1)求c的值;
(2)已知当x=3时,该式子的值为9,试求当x=﹣3时该式子的值;
(3)在第(2)小题的已知条件下,若有3a=5b成立,试比较a+b与c的大小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1 , 得∠A1;∠A1BC和∠A1CD的平分线交于点A2 , 得∠A2;…∠A2016BC和∠A20l6CD的平分线交于点A2017 , 则∠A2017=°. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:

对于甲、乙两人的作法,可判断( )
A. 甲正确,乙错误 B. 甲错误,乙正确
C. 甲、乙均正确 D. 甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的面积为18,点D在线段AC上,点F在线段BC的延长线上,且![]() ,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
,四边形DCFE是平行四边形,则图中阴影部分的面积为( )

A. 8 B. 6 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BC、AD不平行,且∠BAD+∠ADC=270°,E、F分别是AD、BC的中点,已知EF=4,求AB2+CD2的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com