
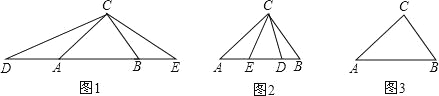
ΓΨΧβΡΩΓΩΘ®1Θ©»γΆΦΘ®1Θ©Θ§‘ΎΓςABC÷–Θ§ABΘΨACΘΨBCΘ§ΓœACB=80ΓψΘ§ΒψDΓΔEΖ÷±π‘ΎœΏΕΈBAΓΔABΒΡ―”≥ΛœΏ…œΘ§«“AD=ACΘ§BE=BCΘ§‘ρΓœDCE= ΘΜ
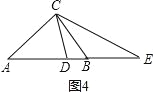
Θ®2Θ©»γΆΦΘ®2Θ©Θ§‘ΎΓςABC÷–Θ§ABΘΨACΘΨBCΘ§ΓœACB=80ΓψΘ§ΒψDΓΔEΖ÷±π‘Ύ±ΏAB…œΘ§«“AD=ACΘ§BE=BCΘ§«σΓœDCEΒΡΕ» ΐΘΜ
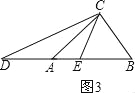
Θ®3Θ©‘ΎΓςABC÷–Θ§ABΘΨACΘΨBCΘ§ΓœACB=80ΓψΘ§ΒψDΓΔEΖ÷±π‘Ύ÷±œΏAB…œΘ§«“AD=ACΘ§BE=BCΘ§‘ρΓœ«σDCEΒΡΕ» ΐΘ®÷±Ϋ”–¥≥ω¥πΑΗΘ©ΘΜ
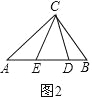
Θ®4Θ©»γΆΦΘ®3Θ©Θ§‘ΎΓςABC÷–Θ§AB=14Θ§AC=15Θ§BC=13Θ§ΒψDΓΔE‘Ύ÷±œΏAB…œΘ§«“AD=ACΘ§BE=BCΘ°«κΗυΨίΧβ“βΑ―ΆΦ–Έ≤ΙΜ≠Άξ’ϊΘ§≤Δ‘ΎΆΦ–ΈΒΡœ¬ΖΫ÷±Ϋ”–¥≥ωΓςDCEΒΡΟφΜΐΘ°Θ®»γΙϊ”–Εύ÷÷«ιΩωΘ§ΆΦ–Έ≤ΜΙΜ”Ο«κΉ‘ΦΚΜ≠≥ωΘ§Ης÷÷«ιΩω”Ο“ΜΗωΆΦ–ΈΒΞΕά±μ ΨΘ©Θ°
ΓΨ¥πΑΗΓΩ(1)ΓΔ130ΓψΘΜ(2)ΓΔ50ΓψΘΜ(3)ΓΔ40ΓψΘΜ(4)ΓΔ252Μρ84Μρ96Μρ72.
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚ(1)ΓΔΗυΨίΒ»―ϋ»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫΓœACD=ΓœDΘ§ΓœBCE=ΓœEΘ§”…»ΐΫ«–ΈΒΡΡΎΫ«ΚΆΒΟΒΫΓœCAB+ΓœCBA=100ΓψΘ§ΗυΨί»ΐΫ«–ΈΒΡΆβΫ«ΒΡ–‘÷ ΒΟΒΫΓœCDA+ΓœBCE=![]() Θ®ΓœCAB+ΓœCBAΘ©=50ΓψΘ§Φ¥Ω…ΒΟΒΫΫα¬έΘΜ
Θ®ΓœCAB+ΓœCBAΘ©=50ΓψΘ§Φ¥Ω…ΒΟΒΫΫα¬έΘΜ
(2)ΓΔΗυΨί»ΐΫ«–ΈΒΡΡΎΫ«ΚΆΚΆΆβΫ«ΒΡ–‘÷ Φ¥Ω…ΒΟΒΫΫα¬έΘΜ(3)ΓΔΒψDΓΔEΖ÷±π‘Ύ÷±œΏAB…œΘ§≥ΐ»ΞΘ®1Θ©Θ®2Θ©ΝΫ÷÷«ιΩωΘ§ΜΙ”–ΝΫ÷÷«ιΩωΘ§»γΆΦ3Θ§”…(1)÷ΣΘ§ΓœD=![]() CABΘ§”…Θ®2Θ©÷ΣΓœCEB=
CABΘ§”…Θ®2Θ©÷ΣΓœCEB=![]() Θ§Ν–ΖΫ≥ΧΦ¥Ω…«σΒΟΫαΙϊΘ°Θ®4Θ©‘ΎΓςABC÷–Θ§AB=14Θ§AC=15Θ§BC=13Θ§ΙΐCΉςCFΓΆAB”κFΘ§ΗυΨίΙ¥Ι…Ε®άμ«σΒΟAB±Ώ…œΒΡΗΏCF=12Θ§»ΜΚσΗυΨί»ΐΫ«–ΈΒΡΟφΜΐΙΪ ΫΦ¥Ω…«Ω¥σΒΡΫα¬έΘ°
Θ§Ν–ΖΫ≥ΧΦ¥Ω…«σΒΟΫαΙϊΘ°Θ®4Θ©‘ΎΓςABC÷–Θ§AB=14Θ§AC=15Θ§BC=13Θ§ΙΐCΉςCFΓΆAB”κFΘ§ΗυΨίΙ¥Ι…Ε®άμ«σΒΟAB±Ώ…œΒΡΗΏCF=12Θ§»ΜΚσΗυΨί»ΐΫ«–ΈΒΡΟφΜΐΙΪ ΫΦ¥Ω…«Ω¥σΒΡΫα¬έΘ°
‘ΧβΫβΈωΘΚ(1)ΓΔΓΏAD=ACΘ§BE=BCΘ§ ΓύΓœACD=ΓœDΘ§ΓœBCE=ΓœEΘ§ ΓΏΓœACB=80ΓψΘ§
ΓύΓœCAB+ΓœCBA=100ΓψΘ§ ΓύΓœCDA+ΓœBCE=![]() Θ®ΓœCAB+ΓœCBAΘ©=50ΓψΘ§ ΓύΓœDCE=130ΓψΘ§
Θ®ΓœCAB+ΓœCBAΘ©=50ΓψΘ§ ΓύΓœDCE=130ΓψΘ§
(2)ΓΔΓΏΓœACB=80ΓψΘ§ ΓύΓœA+ΓœB=100ΓψΘ§ ΓΏAD=ACΘ§BE=BCΘ§ ΓύΓœACD=ΓœADCΘ§ΓœBEC=ΓœBCEΘ§
ΓύΓœADC=![]() Θ§ΓœBEC=
Θ§ΓœBEC=![]() Θ§ ΓύΓœADC+ΓœBEC=180Γψ©¹
Θ§ ΓύΓœADC+ΓœBEC=180Γψ©¹![]() Θ®ΓœA+ΓœBΘ©=130ΓψΘ§ΓύΓœDCE=50ΓψΘΜ
Θ®ΓœA+ΓœBΘ©=130ΓψΘ§ΓύΓœDCE=50ΓψΘΜ
(3)ΓΔΒψDΓΔEΖ÷±π‘Ύ÷±œΏAB…œΘ§≥ΐ»ΞΘ®1Θ©Θ®2Θ©ΝΫ÷÷«ιΩωΘ§ΜΙ”–ΝΫ÷÷«ιΩωΘ§»γΆΦ3Θ§
”…Θ®1Θ©÷ΣΘ§ΓœD=![]() CABΘ§”…Θ®2Θ©÷ΣΓœCEB=
CABΘ§”…Θ®2Θ©÷ΣΓœCEB=![]() Θ§ ΓύΓœCEB=ΓœD+ΓœDCEΘ§
Θ§ ΓύΓœCEB=ΓœD+ΓœDCEΘ§
Γύ![]() =
=![]() CAB+ΓœDCEΘ§ ΓύΓœDCE=40ΓψΘ§ »γΆΦ4Θ§Ά§άμΓœDCE=40ΓψΘΜ
CAB+ΓœDCEΘ§ ΓύΓœDCE=40ΓψΘ§ »γΆΦ4Θ§Ά§άμΓœDCE=40ΓψΘΜ
(4)ΓΔ‘ΎΓςABC÷–Θ§AB=14Θ§AC=15Θ§BC=13Θ§ ΙΐCΉςCFΓΆAB”κFΘ§
(5)‘ρAC2©¹AF2=BC2©¹BF2Θ§Φ¥152©¹AF2=132©¹Θ®14©¹AFΘ©2Θ§ ΫβΒΟΘΚAF=9Θ§ ΓύCF=12Θ§
ΔΌ»γΆΦ1Θ§DE=AB+AC+BC=42Θ§ ΓύSΓςCDE=![]() ΓΝ42ΓΝ12=252ΘΜ
ΓΝ42ΓΝ12=252ΘΜ
ΔΎ»γΆΦ2Θ§DE=AC+BC©¹AB=14Θ§ ΓύSΓςCDE=![]() ΓΝ14ΓΝ12=84ΘΜ
ΓΝ14ΓΝ12=84ΘΜ
Δέ»γΆΦ3Θ§DE=AC+AB©¹BC=16Θ§ ΓύSΓςCDE=![]() ΓΝ16ΓΝ12=96ΘΜ
ΓΝ16ΓΝ12=96ΘΜ
Δή»γΆΦ4Θ§DE=AB+BC©¹AC=12Θ§/span> ΓύSΓςCDE=![]() ΓΝ12ΓΝ12=72Θ°
ΓΝ12ΓΝ12=72Θ°




| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ≈ΉΈοœΏyΘΫΘ≠x2ΒΡΆΦœσ“ΜΕ®Ψ≠Ιΐ( )
A. ΒΎ“ΜΓΔΕΰœσœό B. ΒΎ»ΐΓΔΥΡœσœό
C. ΒΎ“ΜΓΔ»ΐœσœό D. ΒΎΕΰΓΔΥΡœσœό
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΓςABCΘ§A(Θ≠3Θ§2)Θ§B(1Θ§1)Θ§C(Θ≠1Θ§Θ≠2)Θ§œ÷ΫΪΓςABCΤΫ“ΤΘ§ ΙΒψAΒΫΒψ(1Θ§Θ≠2) ΒΡΈΜ÷Ο…œΘ§‘ρΒψBΘ§CΤΫ“ΤΚσΕ‘”ΠΒψΒΡΉχ±ξΖ÷±πΈΣΘ® Θ©
A. (Θ≠3Θ§5)Θ§(Θ≠6Θ§3)
B. (5Θ§Θ≠3)Θ§(3Θ§Θ≠6)
C. (Θ≠6Θ§3)Θ§(Θ≠3Θ§5)
D. (3Θ§Θ≠6)Θ§(5Θ§Θ≠3)
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩaΘ§bΘ§c « Β ΐΘ§ΒψA(aΘΪ1Θ§b)Θ§B(aΘΪ2Θ§c)‘ΎΕΰ¥ΈΚ· ΐyΘΫx2Θ≠2axΘΪ3ΒΡΆΦœσ…œΘ§‘ρbΘ§cΒΡ¥σ–ΓΙΊœΒ «b_____c.(”ΟΓΑΘΨΓ±ΜρΓΑΘΦΓ±ΧνΩ’)
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣBC «Γ―OΒΡœ“Θ§A «Γ―OΆβ“ΜΒψΘ§ΓςABCΈΣ’ΐ»ΐΫ«–ΈΘ§DΈΣBCΒΡ÷–ΒψΘ§MΈΣΓ―O…œ“ΜΒψΘ§≤Δ«“ΓœBMC=60ΓψΘ°

Θ®1Θ©«σ÷ΛΘΚAB «Γ―OΒΡ«–œΏΘΜ
Θ®2Θ©»τEΘ§FΖ÷±π «±ΏABΘ§AC…œΒΡΝΫΗωΕ·ΒψΘ§«“ΓœEDF=120ΓψΘ§Γ―OΒΡΑκΨΕΈΣ2Θ§ ‘Έ BE+CFΒΡ÷Β «ΖώΈΣΕ®÷ΒΘΩ»τ «Θ§«σ≥ω’βΗωΕ®÷ΒΘΜ»τ≤Μ «Θ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥–ΘΤΏΡξΦΕΙ≤320Οϊ―ß…ζ≤ΈΦ” ΐ―ß≤β ‘Θ§ΥφΜζ≥ι»Γ50Οϊ―ß…ζΒΡ≥…Φ®Ϋχ––Ά≥ΦΤΘ§Τδ÷–15Οϊ―ß…ζ≥…Φ®¥οΒΫ”≈–ψΘ§ΙάΦΤΗΟ–ΘΤΏΡξΦΕ―ß…ζ‘Ύ’β¥Έ ΐ―ß≤β ‘÷–¥οΒΫ”≈–ψΒΡ»Υ ΐ¥σ‘Φ”–Θ®ΓΓΓΓΘ©
A. 50»Υ B. 64»Υ C. 90»Υ D. 96»Υ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΒψD‘ΎΓ―OΒΡ÷±ΨΕABΒΡ―”≥ΛœΏ…œΘ§ΒψC‘ΎΓ―O…œΘ§AC=CDΘ§Γ―OΒΡΑκΨΕΈΣ3Θ§![]() ΒΡ≥ΛΈΣΠ–Θ°
ΒΡ≥ΛΈΣΠ–Θ°

Θ®1Θ©÷±œΏCD”κΓ―Oœύ«–¬πΘΩΥΒΟςάμ”…ΓΘ
Θ®2Θ©«σ“θ”Α≤ΩΖ÷ΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΒψM‘Ύy÷αΒΡΉσ≤ύΘ§ΒΫx÷αΓΔy÷αΒΡΨύάκΖ÷±π «3ΚΆ5Θ§‘ρΒψMΒΡΉχ±ξ «( Θ©
A. (Θ≠5Θ§3) B. (Θ≠5Θ§Θ≠3)
C. (5Θ§3)Μρ(Θ≠5Θ§3) D. (Θ≠5Θ§3)Μρ(Θ≠5Θ§Θ≠3)
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σa=2bΘ§»τΘ≠2ΓήbΓήΘ≠1Θ§‘ρaΒΡ»Γ÷ΒΖΕΈß «Θ® Θ©
A. aΓίΘ≠4 B. aΓίΘ≠2
C. Θ≠4ΓήaΓήΘ≠1 D. Θ≠4ΓήaΓήΘ≠2
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com