
 平面直角坐标系中,点A在函数y1=$\frac{2}{x}$(x>0)的图象上,点B在y2=-$\frac{2}{x}$(x<0)的图象上,设A的横坐标为a,B的横坐标为b.
平面直角坐标系中,点A在函数y1=$\frac{2}{x}$(x>0)的图象上,点B在y2=-$\frac{2}{x}$(x<0)的图象上,设A的横坐标为a,B的横坐标为b.分析 (1)如图1,作AC⊥x轴于C,BD⊥x轴于D,先旅游反比例函数解析式确定当A(5,$\frac{2}{5}$),B(-$\frac{2}{5}$,5),再利用反比例函数系数k的几何意义得到S△BOD=S△AOC=1,然后利用S△AOB=S梯形ABDC-S△BOD-S△AOC进行计算;
(2)如图2,AB交y轴于H,根据反比例函数系数k的几何意义,利用S△AOB=S△BOH+S△AOH进行计算即可.
解答 解:(1)如图1,作AC⊥x轴于C,BD⊥x轴于D,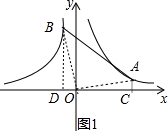
∵|a|=|b|=5,
∴a=5,b=5,
当x=5时,y1=$\frac{2}{x}$=$\frac{2}{5}$,则A(5,$\frac{2}{5}$),
当y=5时,-$\frac{2}{x}$=5,解得x=-$\frac{2}{5}$,则B(-$\frac{2}{5}$,5),
∵S△BOD=$\frac{1}{2}$×2=1,S△AOC=$\frac{1}{2}$×2=1,
∴S△AOB=S梯形ABDC-S△BOD-S△AOC=$\frac{1}{2}$×($\frac{2}{5}$+5)(5+$\frac{2}{5}$)-1-1=$\frac{629}{50}$;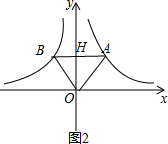
(2)如图2,AB交y轴于H,
∵AB∥x轴,
∴S△AOB=S△BOH+S△AOH=$\frac{1}{2}$×2+$\frac{1}{2}$×2=2.
点评 本题考查了反比例函数系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.


科目:初中数学 来源: 题型:解答题
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 1800元 |
| 第一周 | 4台 | 10台 | 3100元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,矩形OABC的顶点A,C分别在x,y轴的正半轴上,点D为对角线OB的中点,点E(6,n)在边AB上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D,E,且tan∠BOA=$\frac{1}{3}$.
如图所示,矩形OABC的顶点A,C分别在x,y轴的正半轴上,点D为对角线OB的中点,点E(6,n)在边AB上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D,E,且tan∠BOA=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com