
【题目】在平面直角坐标系xOy中,直线l1:y=k1x+6与x轴、y轴分别交于A、B两点,且OB=![]() OA,直线l2:y=k2x+b经过点C(
OA,直线l2:y=k2x+b经过点C(![]() ,1),与x轴、y轴、直线AB分别交于点E、F、D三点.
,1),与x轴、y轴、直线AB分别交于点E、F、D三点.
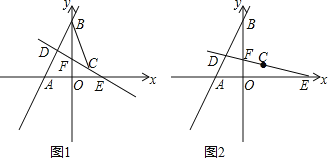
(1)求直线l1的解析式;
(2)如图1,连接CB,当CD⊥AB时,求点D的坐标和△BCD的面积;
(3)如图2,当点D在直线AB上运动时,在坐标轴上是否存在点Q,使△QCD是以CD为底边的等腰直角三角形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.
【答案】(1)y=![]() x+6;(2)D(﹣
x+6;(2)D(﹣![]() ,3),S△BCD=4
,3),S△BCD=4![]() ;(3)存在点Q,使△QCD是以CD为底边的等腰直角三角形,点Q的坐标是(0,±2
;(3)存在点Q,使△QCD是以CD为底边的等腰直角三角形,点Q的坐标是(0,±2![]() )或(6﹣4
)或(6﹣4![]() ,0)或(﹣4
,0)或(﹣4![]() ﹣6,0)
﹣6,0)
【解析】
(1)根据待定系数法可得直线l1的解析式;
(2)如图1,过C作CH⊥x轴于H,求点E的坐标,利用C和E两点的坐标求直线l2的解析式,与直线l1列方程组可得点D的坐标,利用面积和可得△BCD的面积;
(3)分四种情况:在x轴和y轴上,证明△DMQ≌△QNC(AAS),得DM=QN,QM=CN,设D(m,![]() m+6)(m<0),表示点Q的坐标,根据OQ的长列方程可得m的值,从而得到结论.
m+6)(m<0),表示点Q的坐标,根据OQ的长列方程可得m的值,从而得到结论.
解:(1)y=k1x+6,
当x=0时,y=6,
∴OB=6,
∵OB=![]() OA,
OA,
∴OA=2![]() ,
,
∴A(﹣2![]() ,0),
,0),
把A(﹣2![]() ,0)代入:y=k1x+6中得:﹣2
,0)代入:y=k1x+6中得:﹣2![]() k1+6=0,
k1+6=0,
k1=![]() ,
,
∴直线l1的解析式为:y=![]() x+6;
x+6;
(2)如图1,过C作CH⊥x轴于H,
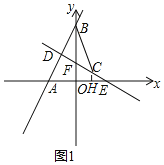
∵C(![]() ,1),
,1),
∴OH=![]() ,CH=1,
,CH=1,
Rt△ABO中,![]() ,
,
∴AB=2OA,
∴∠OBA=30°,∠OAB=60°,
∵CD⊥AB,
∴∠ADE=90°,
∴∠AED=30°,
∴EH=![]() ,
,
∴OE=OH+EH=2![]() ,
,
∴E(2![]() ,0),
,0),
把E(2![]() ,0)和C(
,0)和C(![]() ,1)代入y=k2x+b中得:
,1)代入y=k2x+b中得: ,
,
解得: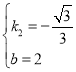 ,
,
∴直线l2:y=![]() x+2,
x+2,
∴F(0,2)即BF=6﹣2=4,
则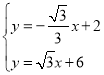 ,解得
,解得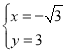 ,
,
∴D(﹣![]() ,3),
,3),
∴S△BCD=![]() BF(xC﹣xD)=
BF(xC﹣xD)=![]() ;
;
(3)分四种情况:
①当Q在y轴的正半轴上时,如图2,过D作DM⊥y轴于M,过C作CN⊥y轴于N,
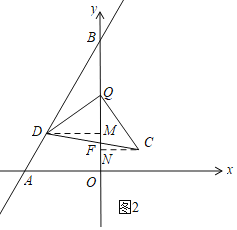
∵△QCD是以CD为底边的等腰直角三角形,
∴∠CQD=90°,CQ=DQ,
∴∠DMQ=∠CNQ=90°,
∴∠MDQ=∠CQN,
∴△DMQ≌△QNC(AAS),
∴DM=QN,QM=CN=![]() ,
,
设D(m,![]() m+6)(m<0),则Q(0,﹣m+1),
m+6)(m<0),则Q(0,﹣m+1),
∴OQ=QN+ON=OM+QM,
即﹣m+1=![]() m+6+
m+6+![]() ,
,
![]() ,
,
∴Q(0,2![]() );
);
②当Q在x轴的负半轴上时,如图3,过D作DM⊥x轴于M,过C作CN⊥x轴于N,
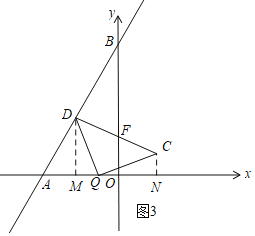
同理得:△DMQ≌△QNC(AAS),
∴DM=QN,QM=CN=1,
设D(m,![]() m+6)(m<0),则Q(m+1,0),
m+6)(m<0),则Q(m+1,0),
∴OQ=QN﹣ON=OM﹣QM,
即![]() m+6-
m+6-![]() =﹣m﹣1,
=﹣m﹣1,
m=5﹣4![]() ,
,
∴Q(6﹣4![]() ,0);
,0);
③当Q在x轴的负半轴上时,如图4,过D作DM⊥x轴于M,过C作CN⊥x轴于N,
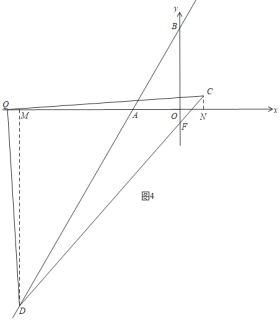
同理得:△DMQ≌△QNC(AAS),
∴DM=QN,QM=CN=1,
设D(m,![]() m+6)(m<0),则Q(m﹣1,0),
m+6)(m<0),则Q(m﹣1,0),
∴OQ=QN﹣ON=OM+QM,
即﹣![]() m﹣6﹣
m﹣6﹣![]() =﹣m+1,
=﹣m+1,
m=﹣4![]() ﹣5,
﹣5,
∴Q(﹣4![]() ﹣6,0);
﹣6,0);
④当Q在y轴的负半轴上时,如图5,过D作DM⊥y轴于M,过C作CN⊥y轴于N,
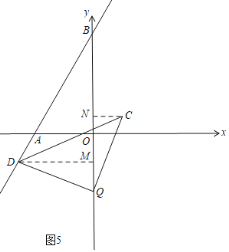
同理得:△DMQ≌△QNC(AAS),
∴DM=QN,QM=CN=![]() ,
,
设D(m,![]() m+6)(m<0),则Q(0,m+1),
m+6)(m<0),则Q(0,m+1),
∴OQ=QN﹣ON=OM+QM,
即﹣![]() m﹣6+
m﹣6+![]() =﹣m﹣1,
=﹣m﹣1,
m=﹣2![]() ﹣1,
﹣1,
∴Q(0,﹣2![]() );
);
综上,存在点Q,使△QCD是以CD为底边的等腰直角三角形,点Q的坐标是(0,±2![]() )或(6﹣4
)或(6﹣4![]() ,0)或(﹣4
,0)或(﹣4![]() ﹣6,0).
﹣6,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=13,AC=12,BC=5,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和等于( )
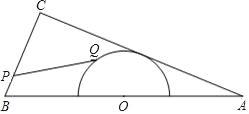
A. 7.5 B. 10 C. 12.5 D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c的图象交x轴于A(4,0),B(﹣1,0)两点,交y轴于点C,连结AC.
x2+bx+c的图象交x轴于A(4,0),B(﹣1,0)两点,交y轴于点C,连结AC.
(1)填空:该抛物线的函数解析式为 ,其对称轴为直线 ;
(2)若P是抛物线在第一象限内图象上的一动点,过点P作x轴的垂线,交AC于点Q,试求线段PQ的最大值;
(3)在(2)的条件下,当线段PQ最大时,在x轴上有一点E(不与点O,A重合),且EQ=EA,在x轴上是否存在点D,使得△ACD与△AEQ相似?如果存在,请直接写出点D的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市市民晚饭后1小时内的生活方式,调查小组设计了“阅读”、“锻炼”、“看电视”和“其它”四个选项,用随机抽样的方法调查了该市部分市民,并根据调查结果绘制成如下统计图.
根据统计图所提供的信息,解答下列问题:
(1)本次共调查了________名市民;
(2)补全条形统计图;
(3)该市共有480万市民,估计该市市民晚饭后1小时内锻炼的人数.
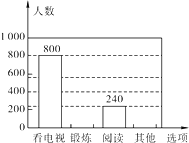

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )

A. ![]() B. 2
B. 2![]() -
-![]() C. 2
C. 2![]() -
-![]() D. 4
D. 4![]() -
-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.
(1)若生产第![]() 档次的产品一天的总利润为
档次的产品一天的总利润为![]() 元(其中
元(其中![]() 为正整数,且1≤
为正整数,且1≤![]() ≤10),求出
≤10),求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC与等腰△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点D、E、C三点在同一条直线上,连接BD.
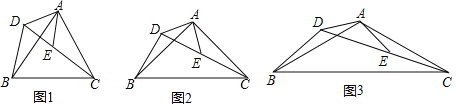
(1)如图1,求证:△ADB≌△AEC
(2)如图2,当∠BAC=∠DAE=90°时,试猜想线段AD,BD,CD之间的数量关系,并写出证明过程;
(3)如图3,当∠BAC=∠DAE=120°时,请直接写出线段AD,BD,CD之间的数量关系式为: (不写证明过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
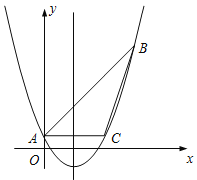
【题目】如图,已知抛物线 y![]() x2 bxc经过△ ABC 的三个顶点,其中点 A(0,1),点 B(9,10),AC∥x 轴,点 P 是直线 AC 下方抛物线上的动点,过点 P 且与 y 轴平行的直线 l 与直线 AB、AC 分别交于点 E、F.
x2 bxc经过△ ABC 的三个顶点,其中点 A(0,1),点 B(9,10),AC∥x 轴,点 P 是直线 AC 下方抛物线上的动点,过点 P 且与 y 轴平行的直线 l 与直线 AB、AC 分别交于点 E、F.
(1)求抛物线的函数表达式;
(2)如图 1,当四边形 AECP 的面积最大时,求点 P 的坐标和四边形 AECP 的最大面积;
(3)如图 2,当点 P 为抛物线的顶点时,在直线 AC 上是否存在点 Q,使得以 C,P,Q 为顶点的三角形与△ ABC 相似?若存在,请直接写出点 Q 的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com