
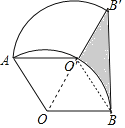
【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )

A. ![]() B. 2
B. 2![]() -
-![]() C. 2
C. 2![]() -
-![]() D. 4
D. 4![]() -
-![]()
【答案】C
【解析】
连接OO′,BO′,根据旋转的性质得到∠OAO′=60°,推出△OAO′是等边三角形,得到∠AOO′=60°,推出△OO′B是等边三角形,得到∠AO′B=120°,得到∠O′B′B=∠O′BB′=30°,根据图形的面积公式即可得到结论.
连接OO′,BO′,
∵将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,
∴∠OAO′=60°,
∴△OAO′是等边三角形,
∴∠AOO′=60°,OO′=OA,
∴点O′中⊙O上,
∵∠AOB=120°,
∴∠O′OB=60°,
∴△OO′B是等边三角形,
∴∠AO′B=120°,
∵∠AO′B′=120°,
∴∠B′O′B=120°,
∴∠O′B′B=∠O′BB′=30°,
∴图中阴影部分的面积=S△B′O′B-(S扇形O′OB-S△OO′B)=![]() ×1×2
×1×2![]() -(
-(![]() -
-![]() ×2×
×2×![]() )=2
)=2![]() -
-![]() .
.
故选C.


 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y1=ax2+bx+c(a≠0)的顶点坐标是(1,4),它与直线y2=x+1的一个交点的横坐标为2.
(1)求抛物线的解析式;
(2)在给出的坐标系中画出抛物线y1=ax2+bx+c(a≠0)及直线y2=x+1的图象,并根据图象,直接写出使y1≥y2的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点A按逆时针方向旋转15°后得到△AB1C1,B1C1交AC于点D,如果AD=![]() ,则△ABC的周长等于( )
,则△ABC的周长等于( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.试回答:

(1)图中等腰三角形是 .猜想:EF与BE、CF之间的关系是 .理由:
(2)如图②,若AB≠AC,图中等腰三角形是 .在第(1)问中EF与BE、CF间的关系还存在吗?
(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-2x-2n=0有两个不相等的实数根,若n<5,且方程的两个实数根都是整数,则n的值为( )
A. n=2
B. n=0或n=1.5或n=4
C. n=4
D. n=0或n=1.5或n=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面的三行单项式
x,2x2,4x3,8x4,16x5…①
﹣2x,4x2,﹣8x3,16x4,﹣32x5…②
2x,﹣3x2,5x3,﹣9x4,17x5…③
根据你发现的规律,完成以下各题:
(1)第①行第8个单项式为 ;第②行第2020个单项式为 .
(2)第③行第n个单项式为 .
(3)取每行的第9个单项式,令这三个单项式的和为A.计算当x=![]() 时,256(A+
时,256(A+![]() )的值.
)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1 (要求A与A1,B与B1,C与C1相对应);
(2)求△ABC的面积;
(3)在直线l上找一点P,使得△PAC的周长最小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读书月活动中,学校准备购买一批课外读物,为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查文化艺术节上,小明参加学校组织的“一站到底”活动,答对最后两道单选题就通关:第一道单选题有A、B、C共3个选项,第二道单选题有A、B、C、D共4个选项,这两道题小明都不会,不过小明还有一次“求助”的机会没有用(使用“求助可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 ;
(2)如果小明决定第一题不使用“求助”,第二题使用“求助”,请用树状图或者列表来分析小明通关的概率;
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD∽四边形GFEH,且∠A=∠G=70°,∠B=55°,∠E=120°,DC=20,HE=15,HG=21.求∠D,∠F的大小和AD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com