
【题目】如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.试回答:

(1)图中等腰三角形是 .猜想:EF与BE、CF之间的关系是 .理由:
(2)如图②,若AB≠AC,图中等腰三角形是 .在第(1)问中EF与BE、CF间的关系还存在吗?
(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
【答案】(1)答案见解析 (2)△EOB、△FOC 存在 (3)答案见解析
【解析】
(1)由AB=AC,可得∠ABC=∠ACB;又已知OB、OC分别平分∠ABC、∠ACB;故∠EBO=∠OBC=∠FCO=∠OCB;根据EF∥BC,可得:∠EOB=∠OBC=∠EBO,∠FOC=∠FCO=∠BCO;由此可得出的等腰三角形有:△AEF、△OEB、△OFC、△OBC、△ABC;
已知了△EOB和△FOC是等腰三角形,则EO=BE,OF=FC,则EF=BE+FC.
(2)由(1)的证明过程可知:在证△OEB、△OFC是等腰三角形的过程中,与AB=AC的条件没有关系,故这两个等腰三角形还成立.所以(1)中得出的EF=BE+FC的结论仍成立.
(3)思路与(2)相同,只不过结果变成了EF=BE-FC.
解:(1)图中是等腰三角形的有:△AEF、△OEB、△OFC、△OBC、△ABC;
EF、BE、FC的关系是EF=BE+FC.理由如下:
∵OB、OC平分∠ABC、∠ACB,
∴∠ABO=∠OBC,∠ACO=∠OCB,
∵EF∥BC,
∴∠EOB=∠OBC=∠EBO,∠FOC=∠OCB=∠FCO,
即EO=EB,FO=FC,
∴EF=EO+OF=BE+CF;
(2)当AB≠AC时,△EOB、△FOC仍为等腰三角形,(1)的结论仍然成立.(证明过程同(1));
(3)△EOB和△FOC仍是等腰三角形,EF=BE-FC.理由如下:
同(1)可证得△EOB是等腰三角形;
∵EO∥BC,
∴∠FOC=∠OCG,
∵OC平分∠ACG,
∴∠ACO=∠FOC=∠OCG,
∴FO=FC,故△FOC是等腰三角形,
∴EF=EO-FO=BE-FC.


科目:初中数学 来源: 题型:
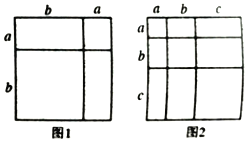
【题目】对于一个图形通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到![]() ,请解答下列问题:
,请解答下列问题:
(1)写出图2中所表示的数学等式;
(2)根据整式乘法的运算法则,通过计算验证上述等a式;
(3)若a+b+c=l0,ab+ac+bc=35,利用得到的结论,求.![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市路桥公司决定对A、B两地之间的公路进行改造,并由甲工程队从A地向B地方向修筑,乙工程队从B地向A地方向修筑.已知甲工程队先施工2天,乙工程队再开始施工,乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.甲、乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数关系如图所示.下列说法:①乙工程队每天修公路240米;②甲工程队每天修公路120米;③甲比乙多工作6天;④A、B两地之间的公路总长是1680米.其中正确的说法有( )
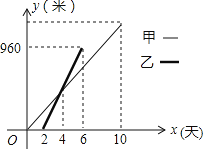
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上.量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为( )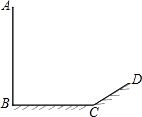
A.9米
B.28米
C.(7+ ![]() )米
)米
D.(14+2 ![]() )米
)米
查看答案和解析>>
科目:初中数学 来源: 题型:
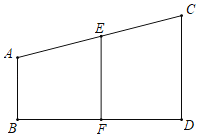
【题目】如图,AB⊥BD,CD⊥BD,∠A与∠AEF互补,以下是证明CD∥EF的推理过程及理由,请你在横线上补充适当条件,完整其推理过程或理由.
证明:∵AB⊥BD,CD⊥BD(已知)
∴∠ABD=∠CDB= ( )
∴∠ABD+∠CDB=180°
∴AB∥ ( )
又∠A与∠AEF互补 ( )
∠A+∠AEF=
∴AB∥ ( )
∴CD∥EF ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快递公司针对新客户优惠收费,首件物品的收费标准为:若重量不超过10千克,则免运费;当重量为![]() 千克时,运费为
千克时,运费为![]() 元;第二件物品的收费标准为:当重量为
元;第二件物品的收费标准为:当重量为![]() 千克时,运费为
千克时,运费为![]() 元。
元。
(1)若新客户所奇首件物品的重量为13千克,则运费是多少元?
(2)若新客户所寄首件物品的运费为32元,则物品的重量是多少千克?
(3)若新客户所寄首件物品与第二件物品的重量之比为2:5,共付运费为60元,则两件物品的重量各是多少千克?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com