
【题目】如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上.量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为( )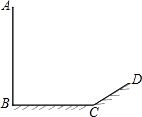
A.9米
B.28米
C.(7+ ![]() )米
)米
D.(14+2 ![]() )米
)米
【答案】D
【解析】解:如图,延长AD交BC的延长线于点F,过点D作DE⊥BC的延长线于点E.

∵∠DCE=30°,CD=8米,
∴CE=CDcos∠DCE=8× ![]() =4
=4 ![]() (米),
(米),
∴DE=4米,
设AB=x,EF=y,
∵DE⊥BF,AB⊥BF,
∴△DEF∽△ABF,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() …①,
…①,
∵1米杆的影长为2米,根据同一时间物高与影长成正比可得 ![]() =
= ![]() …②,
…②,
①②联立,解得x=(14+2 ![]() )米.
)米.
所以答案是:D.
【考点精析】利用相似三角形的应用对题目进行判断即可得到答案,需要熟知测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.


科目:初中数学 来源: 题型:
【题目】某校学生会向全校1900名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图1和图2,请根据相关信息,解答系列问题: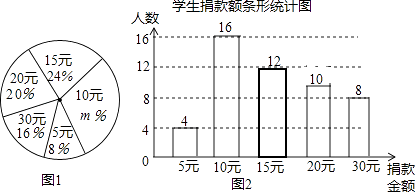
(1)本次接受随机抽样调查的学生人数为人,图1中m的值是 .
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教育部制定《数学课程标准》要求的课程目标之一是通过数学学习,学生能够“初步学会运用数学的思维方式去观察、分析现实社会,去解决日常生活中和其他学科学习中的问题,增强应用数学的意识.”
看过2003年中央电视台春节联欢会的人们都知道,魔术节目很精彩,看后给人以思考、回味,这些看似神秘的魔术节目,很多都依据着一定的科学道理,特别是有些还与我们学习的数学知识有联系,请看下面的小魔术:
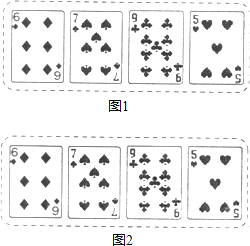
如图2所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180°.魔术师解除蒙具后,看到4张扑克牌如图3所示,他很快确定了哪一张牌被旋转过.
你知道这是怎么回事吗?试利用所学的数学知识,写一篇数学作文解释其中的道理,题目自拟,字数在200~400字之间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元,厂方开展促销活动期间,向客户提供两种优惠方法:①买一套西装送一条领带;②西装和领带均按定价的90%付款。某商店到该服装厂购买西装20件,领带若干条.
(1)领带买多少条时,两种优惠方法相同?
(2)购买50条领带时,应采用哪一种方案更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.试回答:

(1)图中等腰三角形是 .猜想:EF与BE、CF之间的关系是 .理由:
(2)如图②,若AB≠AC,图中等腰三角形是 .在第(1)问中EF与BE、CF间的关系还存在吗?
(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )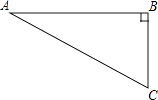
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )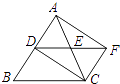
A.矩形
B.菱形
C.正方形
D.梯形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;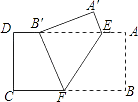
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的一种关系,并给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com