
【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;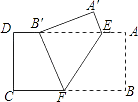
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的一种关系,并给予证明.
【答案】
(1)证明:由题意得B′F=BF,∠B′FE=∠BFE,
在矩形ABCD中,AD∥BC,
∴∠B′EF=∠BFE,
∴∠B′FE=∠B'EF,
∴B′F=B′E,
∴B′E=BF;
(2)解:a,b,c三者存在的关系是a2+b2=c2.
证明:由(1)知B′E=BF=c,A'E=AE=a,
∵B′E=BF=c,
∴在△A'B'E中,∠A=90°,
∴A'E2+A'B'2=B'E2,
∴a2+b2=c2.
【解析】(1)根据折叠的性质得出B′F=BF,∠B′FE=∠BFE,再根据矩形的性质得出AD∥BC,推出∠B′EF=∠BFE,得出∠B′FE=∠B'EF,从而证得B′F=B′E,即可证得结论。
(2)根据题意可知B′E=BF=c,A'E=AE=a,B′E=BF=c,根据勾股定理的逆定理即可证得结论。
【考点精析】利用勾股定理的概念和矩形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等.


科目:初中数学 来源: 题型:
【题目】如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上.量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为( )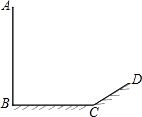
A.9米
B.28米
C.(7+ ![]() )米
)米
D.(14+2 ![]() )米
)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中任意一点P(x0,y0)经平移后对应点为P′(x0+3,y0+4),将△ABC作同样的平移得到△DEF,其中点A与点D,点B与点E,点C与点F分别对应,请解答下列问题:
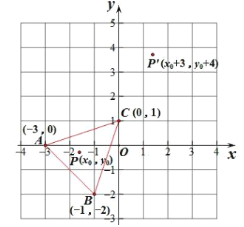
(1)直接写出点D、E、F的坐标;
(2)画出![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ___________,
___________,![]() ______.
______.
(3)若将线段![]() 沿某个方向进行平移得到线段MN,点 B(-1,-2)的对应点为 M ( m,0),则点 C(0,1)的对应点 N 的坐标为________.(用含 m的式子表示)
沿某个方向进行平移得到线段MN,点 B(-1,-2)的对应点为 M ( m,0),则点 C(0,1)的对应点 N 的坐标为________.(用含 m的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,已知AB=AC,∠A=36°,AB的垂直平分线MN交AC于D.在下列结论中:①∠C=72°;②BD是∠ABC的平分线;③∠BDC=100°;④△ABD是等腰三角形;⑤AD=BD=BC.正确的有____.(填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一下正方形.
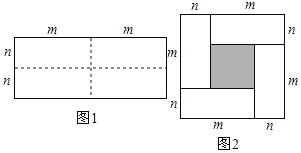
(1)请你用两种不同的方法求图2中阴影部分的面积?
① ②
(2)观察图2,写出三个代数式(m+n)2,(m﹣n)2,4mn之间的等量关系:
(3)根据(2)中的等量关系,解决如下问题:若|a+b﹣7|+|ab﹣6|=0,求(a﹣b)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
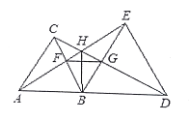
【题目】如图,△ABC和△BDE都是等边三角形,A、B、D三点共线.下列结论:①AE=CD;②BF=BG;③△BFG是等边三角形;④∠AHC=60°.其中正确的有__________(只填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】货车在公路A处加满油后,以每小时60千米的速度匀速行驶,前往与A处相距360千米的B处.下表记录的是货车一次加满油后油箱剩余油量y(升)与行驶时间x(时)之间的关系:

(1)如果y关于x的函数是一次函数,求这个函数解析式(不要求写出自变量的取值范围)
(2)在(1)的条件下,如果货车的行驶速度和每小时的耗油量都不变,货车行驶4小时后到达C处,C的前方12千米的D处有一加油站,那么在D处至少加多少升油,才能使货车到达B处卸货后能顺利返回会D处加油?(根据驾驶经验,为保险起见,油箱内剩余油量应随时不少于10升)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学八年级的篮球队有10名队员![]() 在“二分球”罚篮投球训练中,这10名员各投篮50次的进球情况如下表:
在“二分球”罚篮投球训练中,这10名员各投篮50次的进球情况如下表:
进球数 | 42 | 32 | 26 | 20 | 19 | 18 |
人数 | 1 | 1 | 2 | 1 | 2 | 3 |
针对这次训练,请解答下列问题:
![]() 求这10名队员进球数的平均数、中位数;
求这10名队员进球数的平均数、中位数;
![]() 求这支球队投篮命中率______;
求这支球队投篮命中率______;
![]() 若队员小亮“二分球”的投篮命中率为
若队员小亮“二分球”的投篮命中率为![]() ,请你分析一下小亮在这支球队中的投篮水平.
,请你分析一下小亮在这支球队中的投篮水平.
![]() 投篮命中率
投篮命中率![]() 进球数
进球数![]() 投篮次数
投篮次数![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com