
【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一下正方形.
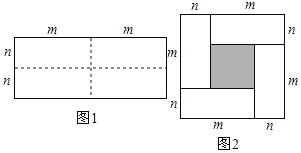
(1)请你用两种不同的方法求图2中阴影部分的面积?
① ②
(2)观察图2,写出三个代数式(m+n)2,(m﹣n)2,4mn之间的等量关系:
(3)根据(2)中的等量关系,解决如下问题:若|a+b﹣7|+|ab﹣6|=0,求(a﹣b)2的值.
【答案】(1)①(m﹣n)2;②(m+n)2﹣4mn;(2)(m﹣n)2=(m+n)2﹣4mn;(3)25.
【解析】
(1)由题意知,阴影部分为一正方形,其边长正好为![]() .根据正方形的面积公式即可求出图中阴影部分的面积,也可以用大正方形的面积减去四个小长方形的面积由图形可得:
.根据正方形的面积公式即可求出图中阴影部分的面积,也可以用大正方形的面积减去四个小长方形的面积由图形可得:
(2)大正方形的面积减去四个小长方形的面积正好等于图中阴影部分的面积.
(3)![]() 正好表示大正方形的面积,
正好表示大正方形的面积,![]() 正好表示阴影部分小正方形的面积,
正好表示阴影部分小正方形的面积,![]() 正好表示一个小长方形的面积.根据(2)中的等式代入计算即可.
正好表示一个小长方形的面积.根据(2)中的等式代入计算即可.
解:(1)①由图可知,阴影部分是一个正方形,边长为m﹣n
∴阴影部分的面积为:(m﹣n)2;
②由图形知,阴影部分的面积=大正方形的面积减去四个小长方形的面积,
∴阴影部分的面积为(m+n)2﹣4mn;
故答案为:①(m﹣n)2;②(m+n)2﹣4mn;
(2)由(1)知(m﹣n)2 = (m+n)2﹣4mn,
故答案为:(m﹣n)2=(m+n)2﹣4mn;
(3)∵|a+b﹣7|+|ab﹣6|=0
∴a+b=7,ab=6,
当a+b=7,ab=6时,
(a-b)2
=(a+b)2-4ab
=72-4×6
=49﹣24
=25,


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P为四边形ABCD边上的任意一点,当∠BPC=30°时,CP的长为 . 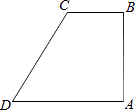
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;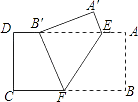
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的一种关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个等腰直角三角形按图示方式依次翻折,则下列说法正确的个数有( )

①DF平分∠BDE;②△BFD是等腰三角形;;③△CED的周长等于BC的长.
A. 0个; B. 1个; C. 2个; D. 3个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸上的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形.在建立平面直角坐标系后,点B的坐标为(﹣2,﹣1).
(1)把△ABC向左平移4格后得到△A1B1C1,画出△A1B 1C1并写出点A1的坐标;
(2)把△ABC绕点C按顺时针旋转90°后得到△A2B2C,画出△A2B2C的图形并写出点A2的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com