
【题目】如图,在![]() 中,
中,![]() ,点D为AC的中点,过点C作
,点D为AC的中点,过点C作![]() 于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取
于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取![]() ,连接BG、DF.
,连接BG、DF.
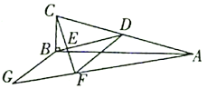
(1)证明:四边形BDFG是菱形;
(2)若![]() ,
,![]() ,求线段AG的长度.
,求线段AG的长度.
科目:初中数学 来源: 题型:
【题目】随着我市社会经济的发展和交通状况的改善,我市的旅游业得到了高速发展,某旅游公司对我市一企业个人旅游年消费情况进行问卷调查,随机抽查部分员工,记录每个人年消费金额,并将调查数据适当整理,绘制成尚不完整的表和图(如图).
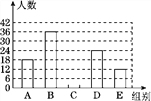
组别 | 个人年消费金额x/元 | 频数(人数) | 频率 |
A | x≤2 000 | 18 | 0.15 |
B | 2 000<x≤4 000 | a | b |
C | 4 000<x≤6 000 | ||
D | 6 000<x≤8 000 | 24 | 0.20 |
E | x>8 000 | 12 | 0.10 |
合计 | c | 1.00 |
根据以上信息回答下列问题:
(1)a=________,b=________,c=________,并将条形统计图补充完整;
(2)在这次调查中,个人年消费金额的中位数出现在________组;
(3)若这个企业有3 000名员工,请你估计个人旅游年消费金额在6 000元以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在今年2月底以每袋23元的成本价收购一批农产品准备向外销售,当此农产品售价为每袋36元时,3月份销售125袋,4、5月份该农产品十分畅销,销售量持续走高.在售价不变的基础上,5月份的销售量达到180袋.设4、5这两个月销售量的月平均增长率不变.
(1)求4、5这两个月销售量的月平均增长率;
(2)6月份起,该商店采用降价促销的方式回馈顾客,经调查发现,该农产品每降价1元/袋,销量就增加4袋,当农产品每袋降价多少元时,该商店6月份获利1920元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设a+b![]() (其中a、b、m、n均为整数),
(其中a、b、m、n均为整数),
则有:a+b![]() ,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b
,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() ,用含m、n的式子分别表示a、b得:a= ,b= ;
,用含m、n的式子分别表示a、b得:a= ,b= ;
(2)利用所探索的结论,用完全平方式表示出:7+4![]() = .
= .
(3)请化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).
ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).

A.AE=CFB.DE=BFC.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
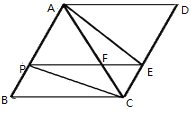
【题目】如图,在四边形ABCD中,![]() ,
,![]() ,连接AC,点P、E分别在AB、CD上,连接PE,PE与AC交于点F,连接PC,
,连接AC,点P、E分别在AB、CD上,连接PE,PE与AC交于点F,连接PC,![]()
![]() ,
,![]() .
.
(1)判断四边形PBCE的形状,并说明理由;
(2)求证:![]() ;
;
(3)当P为AB的中点时,四边形APCE是什么特殊四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
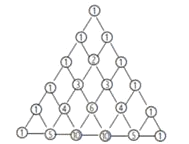
【题目】我国古代数学领域有些研究成果曾位居世界前列,其中“杨辉三角”就是一例.南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中,用图中的三角形解释二项和的乘方规律.杨辉三角两腰上的数都是1,其余每个数都为它的上方(左右)两数之和,这个三角形给出了(a+b)n(n=1,2,3,4,5)的展开式(按a的次数由大到小的顺序)的系数规律.例如,此三角形中第3行的3个数1,2,1,恰好对应着(a+b)2=a2+2ab+b2展开式中各项的系数:第4行的4个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中各项的系数,等等.利用上面呈现的规律填空:(a+b)6=a6+6a5b+________+20a3b3+15a2b4+ ________+b6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,七(1)班的小明等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话,试根据对话中的信息,解答下列问题:
儿子:爸爸,成人门票是每张20元;学生门票是五折优惠;
团体票(16人及16人以上),按成人票的六折优惠.
爸爸:我们成人、学生一共12人,共需200元.
(1)设小明他们一共去了学生![]() 人,则成人购买门票的总费用为: 元;(用含
人,则成人购买门票的总费用为: 元;(用含![]() 的代数式表示)
的代数式表示)
(2)七(1)班小明他们一共去了几个成人、几个学生?
(3)正在购票时,小明发现七(2)班的小军等10名同学和他们的7名家长共17人也来购票,他们准备联合一起购买门票,请你为这29人的团队设计出最省的购票方案(直接写出方案即可,无需讨论),并求出此时的购票费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为4,点
的边长为4,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上运动,且保持
边上运动,且保持![]() ,连接
,连接![]() ,
,![]() ,
,![]() .在此运动过程中,下列结论:①
.在此运动过程中,下列结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积保持不变;④当
的面积保持不变;④当![]() 时,
时,![]() ,其中正确的结论是( )
,其中正确的结论是( )
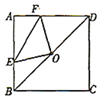
A.①②B.②③C.①②④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com