
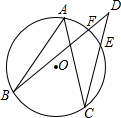
 如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,比较∠BAC与∠BDC的大小,并说明理由.
如图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,比较∠BAC与∠BDC的大小,并说明理由.  全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A(m,n)、点B在反比例函数y=$\frac{k}{x}$(x>0)的图象上,∠OAB=90°,AO=AB,求$\frac{m}{n}$的值.
如图,已知点A(m,n)、点B在反比例函数y=$\frac{k}{x}$(x>0)的图象上,∠OAB=90°,AO=AB,求$\frac{m}{n}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
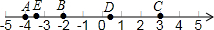 根据如图所示的数轴,把下列表格补充完整,指出哪一点表示的数的绝对值最大.
根据如图所示的数轴,把下列表格补充完整,指出哪一点表示的数的绝对值最大.| 点 | A | B | C | D | E |
| 有理数 | -4 | -2 | 0.5 | ||
| 相反数 | 2 | -3 | |||
| 绝对值 | 4 | 3.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2,3,$\sqrt{13}$是一组勾股数 | |
| B. | 估算得$\sqrt{5}$$<\root{3}{7}$ | |
| C. | 无理数是无限小数 | |
| D. | 在海面上知道一个方位角就可以确定一个目标的位置 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com