
【题目】某气象研究中心观测到一场沙尘暴从发生到减弱的过程,开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速y(千米/小时),时间x(小时)成反比例关系地慢慢减弱,结合风速与时间的图象,回答下列问题:

(1)这场沙尘暴的最高风速是多少?最高风速维持了多长时间;
(2)求出当x≥20时,风速y(千米/小时)与时间x(小时)之间的函数关系?
(3)在这次沙尘暴的形成过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻是“危险时刻”.问这次风暴的整个过程中,“危险时刻”一共有多长时间?
【答案】(1)32、10;(2)![]() ;(3)59.5小时
;(3)59.5小时
【解析】
(1)由速度=增加幅度×时间可得4时风速为8千米/时,10时达到最高风速,为32千米/时,与x轴平行的一段风速不变,最高风速维持时间为20﹣10=10小时;
(2)设y=![]() ,将(20,32)代入,利用待定系数法即可求解;
,将(20,32)代入,利用待定系数法即可求解;
(3)由于4时风速为8千米/时,而4小时后,风速变为平均每小时增加4千米,所以4.5时风速为10千米/时,再将y=10代入(2)中所求函数解析式,求出x的值,再减去4.5,即可求解.
解:(1)0~4时,风速平均每小时增加2千米,所以4时风速为8千米/时;
4~10时,风速变为平均每小时增加4千米,10时达到最高风速,为8+6×4=32千米/时,
10~20时,风速不变,最高风速维持时间为20﹣10=10小时;
答:这场沙尘暴的最高风速是32千米/时,最高风速维持了10小时;
(2)设y=![]() ,
,
将(20,32)代入,得32=![]() ,
,
解得k=640.
所以当x≥20时,风速y(千米/小时)与时间x(小时)之间的函数关系为y=![]() ;
;
(3)∵4时风速为8千米/时,而4小时后,风速变为平均每小时增加4千米,
∴4.5时风速为10千米/时,
将y=10代入y=![]() ,
,
得10=![]() ,
,
解得x=64,
64﹣4.5=59.5(小时).
故沙尘暴的风速从开始形成过程中的10千米/小时到最后减弱过程中的10千米/小时,共经过59.5小时.
答:这次风暴的整个过程中,“危险时刻”一共经过59.5小时.


科目:初中数学 来源: 题型:
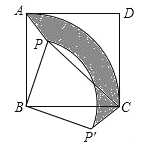
【题目】已知:如图,点P是正方形ABCD内一点,连接PA、PB、PC.
(1)将△PAB绕点B顺时针旋转90°得到△P'CB,若AB=m,PB=n(n<m).求△PAB旋转过程中边PA扫过区域(阴影部分)的面积;
(2)若PA=![]() ,PB=
,PB=![]() ,∠APB=135°,求PC的长.
,∠APB=135°,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有3个带号码的球,球号分别为2,3,4,这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏,游戏规则如下:
先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号。将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数。若该两位数能被4整除,则甲胜,否则乙胜.
问:这个游戏公平吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批日用品,若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数![]() (件)与价格
(件)与价格![]() (元/件)之间满足一次函数关系.
(元/件)之间满足一次函数关系.
(1)试求:y与x之间的函数关系式;
(2)这批日用品购进时进价为4元,则当销售价格定为多少时,才能使每月的润最大?每月的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于AB)的长方形花圃.

(1)设花圃的一边AB为xm,则BC的长可用含x的代数式表示为______m;
(2)当AB的长是多少米时,围成的花圃面积为63平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(-1,5),B(﹣1,0),C(﹣4,3).
(1)在图中画出△ABC关于y轴对称的图形△A1B1C1;(其中A1、B1、C1分别是A、B、C的对应点,不写画法.)
(2)写出点A1、B1、C1的坐标;
(3)求出△A1B1C1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.

(1)当a=﹣![]() 时,①求h的值;②通过计算判断此球能否过网.
时,①求h的值;②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,过点O作两条射线OM、ON,且∠AOM=∠CON=90°

(1)若OC平分∠AOM,求∠AOD的度数.
(2)若∠1=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(4分)如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )

A.转化思想
B.三角形的两边之和大于第三边
C.两点之间,线段最短
D.三角形的一个外角大于与它不相邻的任意一个内角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com