
【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,且点A(0,2),点C(1,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D.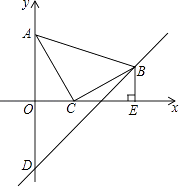
(1)求证:△AOC≌△CEB;
(2)求△ABD的面积.
【答案】
(1)证明:∵BE⊥CE,
∴∠BEC=90°,
∵△ABC是等腰直角三角形,
∴AC=BC,∠ACB=90°.
∵∠O=∠ACB=90°,
∴∠OAC+∠ACO=90°,∠ACO+∠BCE=90°,
∴∠OAC=∠BCE.
在RtAOC和Rt△CEB中,
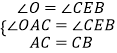 ,
,
∴RtAOC≌Rt△CEB (AAS)
(2)如图:作BF⊥y轴于F点.

∵RtAOC≌Rt△CEB,
∴CE=OA=2,BE=OC=1,
∴OE=CC+CE=1+2=3,
即B(3,1),BF=3.
将B点坐标代入y=x+b,得
3+b=1,
解得b=﹣2,
直线BD的解析式为y=x﹣2,
当x=0时,y=﹣2,即D(0,﹣2).
S△ABD= ![]() ADBF=
ADBF= ![]() ×[2﹣(﹣2)]×3=6
×[2﹣(﹣2)]×3=6
【解析】(1)根据等腰直角三角形的性质,可得AC=BC,∠ACB=90°,根据余角的性质,可得∠OAC=∠BCE,根据AAS,可得答案;(2)根据全等三角形的性质,可得B点坐标,根据待定系数法,可得b的值,根据三角形的面积公式,可得答案.
【考点精析】认真审题,首先需要了解三角形的面积(三角形的面积=1/2×底×高),还要掌握等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角))的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,点P(![]() +1,
+1, ![]() ﹣1)在双曲线y=kx-1(x>0)上.
﹣1)在双曲线y=kx-1(x>0)上.
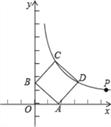
(1)求k的值;
(2)若正方形ABCD的顶点C,D在双曲线y=kx-1(x>0)上,顶点A,B分别在x轴和y轴的正半轴上,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是( ) 
A.y=2x+3
B.y=x﹣3
C.y=2x﹣3
D.y=﹣x+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的袋子中只有 3 个黑球和 4 个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出 4 个球,下列事件是不可能事件的是( )
A.摸出的全部是黑球B.摸出 2 个黑球,2 个白球
C.摸出的全部是白球D.摸出的有 3 个白球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形,AC、DE相交于点O. 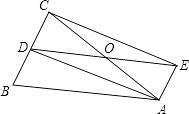
(1)求证:四边形ADCE是矩形.
(2)若∠AOE=60°,AE=4,求矩形ADCE对角线的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com