

解:(1)因为OD、OE分别是∠AOC、∠BOC的平分线,
∠AOC=48°,∠BOC=42°,
所以∠DOC= 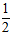 ∠AOC=
∠AOC= 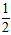 ×48°=24°,
×48°=24°,
∠COE= 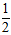 ∠BOC=
∠BOC= 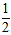 ×42°=21°.
×42°=21°.
所以∠DOE=∠DOC+∠EOC=24°+21°=45°
(2)因为OD 、OE 分别是∠AOC 、∠BOC 的平分线,
所以∠DOC=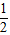 ∠AOC ,∠COE=
∠AOC ,∠COE= ∠BOC .
∠BOC .
所以∠DOE= ∠DOC+ ∠EOC=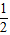 ∠AOC+
∠AOC+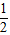 ∠BOC=
∠BOC=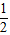 (∠AOC+ ∠BOC )=
(∠AOC+ ∠BOC )=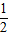 ∠AOB .
∠AOB .
因为∠AOB= ∠AOC+ ∠BOC=48 °+42 °=90 °,
所以∠DOE=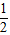 ∠AOB=
∠AOB=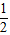 ×90 °=45 °.
×90 °=45 °.
故∠DOE 的大小不变,仍为45 °
(3)∠DOE的大小不变,仍为45。
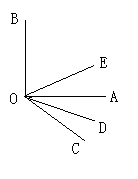
理由:如图,因为OD、OE分别是∠AOC、∠BOC的平分线
所以∠DOC=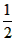 ∠AOC ,∠COE=
∠AOC ,∠COE=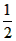 ∠BOC
∠BOC
所以∠DOE=∠EOC-∠DOC =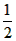 ∠BOC-
∠BOC-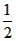 ∠AOC =
∠AOC =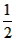 (∠BOC-∠AOC) =
(∠BOC-∠AOC) =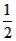 ∠AOB
∠AOB
因为∠AOB=90°
所以∠DOE= ∠AOB=
∠AOB=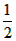 ×90°=45°
×90°=45°
故∠DOE的大小不变,仍为45°。


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 补全下列解题过程
补全下列解题过程| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源:2014湘教版七年级上册(专题训练 状元笔记)数学:第四章 图形的认识 几何图形 线段、射线、直线 湘教版 题型:044
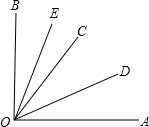
如图,OD是∠AOC的平分线,OE是∠BOC的平分线.

(1)如果∠AOC=48°,∠BOC=42°,求∠DOE的度数;
(2)如图∠AOB的大小不变,与(1)相同,而射线OC在∠AOB的内部绕点O旋转,∠DOE的大小是否发生变化?若不变,请求出其度数;
(3)如果∠AOB的大小仍不变,而射线OC在∠AOB的外部绕点O旋转(∠AOC不大于90°),OD是∠AOC的平分线,OE是∠BOC的平分线,请画出相应的图形,此时∠DOE的大小是否发生变化?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com