
【题目】如图,在△ABC中,∠ACB=90°,BC=6cm,AC=8cm,点O为AB的中点,连接CO.点M在CA边上,从点C以1cm/秒的速度沿CA向点A运动,设运动时间为t秒. 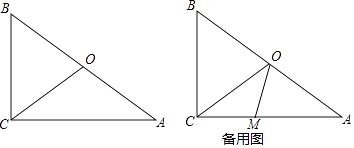
(1)当∠AMO=∠AOM时,求t的值;
(2)当△COM是等腰三角形时,求t的值.
【答案】
(1)解:∵AC=8,BC=6,∠ACB=90°,
∴AB= ![]() =10,
=10,
∵O为AB中点,
∴AO= ![]() AB=5,
AB=5,
∵AO=AM,
∴AM=5,
∴CM=3,
∴t=3;
(2)解:①当CO=CM时,CM=5,
∴t=5
②当MC=MO时,t2=32+(4﹣t)2,
解得:t= ![]() ;
;
③当CO=OM时,M与A点重合,
∴t=8;
综上所述,当△COM是等腰三角形时,t的值为5或 ![]() 或81.
或81.
【解析】(1)由勾股定理求出AB,由直角三角形的性质得出AO=5,求出AM=5,得出CM=3即可;(2)分三种情况讨论,分别求出t的值即可.
【考点精析】利用等腰三角形的性质和勾股定理的概念对题目进行判断即可得到答案,需要熟知等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( ) 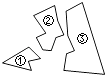
A.带①去
B.带②去
C.带③去
D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学之道在于悟.希望同学们在问题(1)解决过程中有所悟,再继续探索研究问题(2).
(1)如图①,∠B=∠C,BD=CE,AB=DC. ①求证:△ADE为等腰三角形.
②若∠B=60°,求证:△ADE为等边三角形.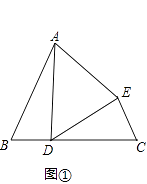
(2)如图②,射线AM与BN,MA⊥AB,NB⊥AB,点P是AB上一点,在射线AM与BN上分别作点C、点 D 满足:△CPD为等腰直角三角形.(要求:利用直尺与圆规,不写作法,保留作图痕迹) 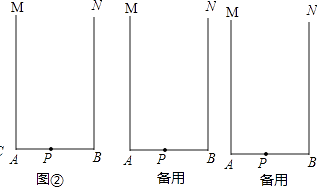
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com