
����Ŀ��ѧ֮��������ϣ��ͬѧ�������⣨1������������������ټ���̽���о����⣨2����
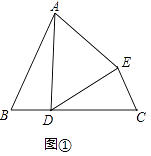
��1����ͼ�٣���B=��C��BD=CE��AB=DC�� ����֤����ADEΪ���������Σ�
������B=60�㣬��֤����ADEΪ�ȱ������Σ�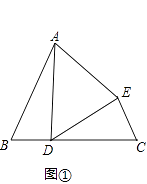
��2����ͼ�ڣ�����AM��BN��MA��AB��NB��AB����P��AB��һ�㣬������AM��BN�Ϸֱ�����C���� D ���㣺��CPDΪ����ֱ�������Σ���Ҫ������ֱ����Բ�棬��д������������ͼ�ۼ��� 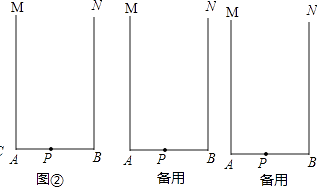
���𰸡�
��1���⣺��֤�����ߡ�B=��C��BD=CE��AB=DC��
���ABD��DCE��
��AB=DC��
���ADE����������
�ڡߡ�ABD�ա�DCE��
���BAD=��CDE��
�ߡ�ADC�ǡ�ABD����ǣ�
���ADC=��B+��BAD��
�ߡ�ADC=��ADE+��EDC��
�֡ߡ�BAD=��CDE��
���ADE=��B=60�㣬
�������ADEΪ�ȱ������Σ�
��2���⣺�����ֽ������ͼ��ʾ��
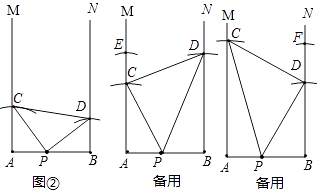
����������1�����ȸ��ݡ�B=��C��BD=CE��AB=DC���ж���ABD��DCE���ó�AB=DC�������õ���ADEΪ���������Σ��ڸ��ݡ�ABD�ա�DCE���ó���BAD=��CDE���ٸ��ݡ�ADC=��B+��BAD����ADC=��ADE+��EDC���õ���ADE=��B=60�㣬����ж�������ADEΪ�ȱ������Σ���2��������������ۣ���CPDΪֱ�Ƕ��㣻��PCD��ֱ�Ƕ��㣻��PDC��ֱ�Ƕ��㣬�ֱ���л�ͼ���ɣ���һ�������ʹ��AP=BD��BP=AC���ڶ��������ʹ��AC=AB��CE=AP��BD=AE�������������ʹ��BD=AB��DF=BP��AC=BF��
�����㾫����������Ŀ����֪���������õ���ֱ�������κ͵��������ε��ж������֪ʶ���Եõ�����Ĵ𰸣���Ҫ���յ���ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣻���һ������������������ȣ���ô�����������Եı�Ҳ��ȣ���ƣ��ȽǶԵȱߣ�������ж�����������֤��ͬһ���������еı���ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��B����������������ʾ�����ֱ�Ϊa��b����A��B�����ľ���ɼ�Ϊ|a��b|��
��1����ͼ����A��B����������������ʾ�����ֱ�Ϊ��2��4����A��B����ľ���Ϊ��![]()
��2����A,B����ֱ���ÿ��3����λ���Ⱥ�ÿ��1����λ���ȵ��ٶ�ͬʱ�������������˶������˶�ʱ��Ϊt�룬����������⣺
���˶�t���A������ʾ����Ϊ �� B������ʾ����Ϊ�����𰸾��ú�t�Ĵ���ʽ��ʾ��
�ڵ�tΪ��ֵʱ��A��B����ľ���Ϊ4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڡ�ABC�У�AB=AC����ACΪֱ���ġ�O��BC���ڵ�D��DE��AB������ΪE��ED���ӳ�����AC���ӳ��߽��ڵ�F��

��1����֤��DE�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ4��BE=2�����F�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�
�������Ϲ����˿����仯������ᾭ�ú�������ᵽ�ı�����һ�����һ����65�꼰���������˿�����ռ���˿ڱ�������7��ʱ����ζ��������һ�����������仯���Ӿ��ýǶȣ�һ����á������˿ڸ����ȡ�����ӳ�˿����仯���ĺ������ν�������˿ڸ����ȡ���ָij��Χ�˿��У������˿�����65�꼰�����˿��������Ͷ������˿�����15-64���˿�����֮�ȣ�ͨ���ðٷֱȱ�ʾ�����Ա���ÿ100���Ͷ������˿�Ҫ���������������ˡ�
�����Ǹ����ҹ���������˿��������������ͳ��ͼ��ͳ�Ʊ���
2011-2014��ȫ���˿�����ֲ�ͼ

2011-2014��ȫ���˿�����ֲ���
2011�� | 2012�� | 2013�� | 2014�� | |
0-14���˿�ռ���˿ڵİٷֱ� | 16.4�� | 16.5�� | 16.4�� | 16.5�� |
15-64���˿�ռ���˿ڵİٷֱ� | 74.5�� | 74.1�� | 73.9�� | 73.5�� |
65�꼰�����˿�ռ���˿ڵİٷֱ� | m | 9.4�� | 9.7�� | 10.0�� |
*����ͼ�������ݾ�Ϊ��ĩ�����ݡ�
�������ϲ��Ͻ���������⣺
��1��2011��ĩ���ҹ����˿�ԼΪ_______�ڣ�ȫ���˿�����ֲ�����m��ֵΪ_______��
��2������Ŀǰ�ҹ����˿���Ȼ�������Ʋ⣬��2027��ĩ�ҹ�Լ��14.60���ˡ�����0-14���˿�ռ���˿ڵİٷֱ�һֱ�ȶ���16.5����15-64����˿�һֱ�ȶ���10�ڣ���ô2027��ĩ�ҹ�0-14���˿�ԼΪ_______�ڣ��������˿ڸ����ȡ�ԼΪ_______�� ����ȷ��1����
��3��2016��1��1�����ҹ���ʼʩ�С�ȫ����������ߣ�һ�Է��������������ӡ���δ��10���������������������ߣ���_______����ᡱ���ᡱ�����ҹ��ġ������˿ڸ����ȡ�����Ӱ�졣
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ�У�������ʽa+1���ǣ�������
A.a2��1
B.2a2+4a+2
C.a2+a��2
D.a2��2a��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AEƽ�֡�BAD��DEƽ�֡�ADC�� 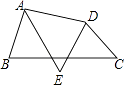
��1�������B+��C=120�㣬���AED�Ķ���= �� ��ֱ��д�������
��2�����ݣ�1���Ľ��ۣ������B+��C���AED֮��Ĺ�ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90�㣬BC=6cm��AC=8cm����OΪAB���е㣬����CO����M��CA���ϣ��ӵ�C��1cm/����ٶ���CA���A�˶������˶�ʱ��Ϊt�룮 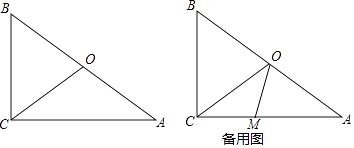
��1������AMO=��AOMʱ����t��ֵ��
��2������COM�ǵ���������ʱ����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����������,��20��ѡ����.���ֱ���:��1���5��,��1���2��,�����ⲻ����Ҳ���۷�.С����������δ��.���ٴ�Լ�����,�ֲܷŲ������60��.��С�����ٴ�Ե�������( )
A.11�� B��12�� C.13�� D.14��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����һ�ų����ε�ֽƬABCD�ضԽ���BD�۵�����C����E����BE��AD�ڵ�F�� 
��1����֤��FB=FD��
��2����ͼ2������AE����֤��AE��BD�� 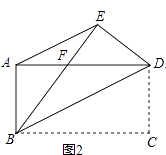
��3����ͼ3���ӳ�BA��DE�ཻ�ڵ�G������GF���ӳ���BD�ڵ�H����֤��GH��ֱƽ��BD�� 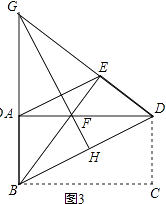
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com